题目内容
在实数R中定义一种运算“*”,具有下列性质:
(1)对任意a,b∈R,a*b=b*a;
(2)对任意a∈R,a*0=a;
(3)对任意a,b,c∈R,(a*b)*c=c*(ab)+(a*c)+(b*c)-2c
则函数f(x)=x*
的单调递减区间是( )
(1)对任意a,b∈R,a*b=b*a;
(2)对任意a∈R,a*0=a;
(3)对任意a,b,c∈R,(a*b)*c=c*(ab)+(a*c)+(b*c)-2c
则函数f(x)=x*
| x |
| 2 |
A、(-∞,
| ||
B、[-
| ||
C、(-∞,
| ||
D、(-∞,-
|
分析:准确理解运算“*”的性质:①满足交换律,②a*0=a;③,(a*b)*c=c*(ab)+(a*c)+(b*c)-2c,故有:a*b=(a*b)*0=0*(ab)+(a*0)+(b*0)-2×0;代入可得答案.
解答:解:在(3)中,令c=0,则 a*b=ab+a+b?f(x)=x*
=
+
=
(x+
)2-
,
易知函数f(x)的单调递减区间为 (-∞,-
),
故选D.
| x |
| 2 |
| x2 |
| 2 |
| 3x |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
易知函数f(x)的单调递减区间为 (-∞,-
| 3 |
| 2 |
故选D.
点评:此题是个中档题.本题是一个新定义运算型问题,解答的关键是对函数的单调性等有关性质的理解以及同学们类比运算解决问题的能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
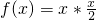 x∈R的单调递减区间是________.
x∈R的单调递减区间是________.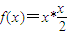 x∈R的单调递减区间是 .
x∈R的单调递减区间是 .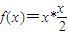 x∈R的单调递减区间是 .
x∈R的单调递减区间是 .