题目内容
4. 如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.
如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.(1)求证:PA=PC;
(2)若圆O的半径为3,PO=5,求线段AC的长度.
分析 (1)根据弦切角定理,可得∠PAB=∠ACB,根据圆周角定理可得∠BAC=90°,结合BC⊥OP,根据同角的余角相等及对顶角相等可得∠PDA=∠PAB,即△PAD为等腰三角形;
(2)利用切割线定理求出PA,再求出cos∠AOP,利用余弦定理,即可得出结论.
解答 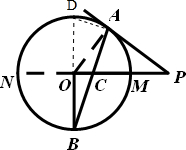 (1证明:∵PA与圆O相切于点A,
(1证明:∵PA与圆O相切于点A,
∴∠PAB=∠ADB
∵BD为圆O的直径,
∴∠BAD=90°
∴∠ADB=90°-∠B
∵BD⊥OP,
∴∠BCO=90°-∠B
∴∠BCO=∠PCA=∠PAB
即△PAC为等腰三角形
∴PA=PC;…(5分)
(2)解:假设PO与圆O相交于点M,延长PO交圆O于点N.
∵PA与圆O相切于点A,PMN是圆O的割线,
∴PA2=PM•PN=(PO-OM)(PO+ON).
∵PO=5,OM=ON=3,∴PA=4.
由(1)知PC=PA=4,∴OC=1.
在Rt△OAP中,cos∠AOP=$\frac{OA}{OP}$=$\frac{3}{5}$.
∴AC2=9+1-2×3×1×$\frac{3}{5}$=$\frac{32}{5}$.
∴AC=$\frac{4\sqrt{10}}{5}$.…(10分)
点评 本题考查的知识点是弦切角定理,圆周角定理,等腰三角形的判定,相似三角形的判定与性质,属于中档题.

练习册系列答案
相关题目
15.从点P出发的三条射线PA,PB,PC两两成60°角,且分别与球O相切于A,B,C三点,若OP=$\sqrt{3}$,则球的体积为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{8π}{3}$ |
12.某工厂从外地连续两次购得A,B两种原料,购买情况如右表:现计划租用甲,乙两种货车共8辆将两次购得的原料一次性运回工厂.
(1)A,B两种原料每吨的进价各是多少元?
(2)已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A,B两种原料各2吨.如何安排甲,乙两种货车?写出所有可行方案.
(3)若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元.设安排甲种货车x辆,总运费为W元,求W(元)与x(辆)之间的函数关系式;在(2)的前提下,x为何值时,总运费W最小,最小值是多少元?
| A(吨) | B(吨) | 费用(元) | |
| 第一次 | 12 | 8 | 33600 |
| 第二次 | 8 | 4 | 20800 |
(2)已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A,B两种原料各2吨.如何安排甲,乙两种货车?写出所有可行方案.
(3)若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元.设安排甲种货车x辆,总运费为W元,求W(元)与x(辆)之间的函数关系式;在(2)的前提下,x为何值时,总运费W最小,最小值是多少元?
16.已知集合A={x∈R|0<x≤2},集合B={x∈R|(1-x)(2+x)>0},则(∁RA)∩B=( )
| A. | ∅ | B. | (2,+∞) | C. | (-2,0) | D. | (-2,0] |
14.设直线l与抛物线y2=4x相交于A、B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点,若这样的直线l恰有4条,则r的取值范围是( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |