题目内容
已知椭圆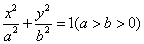 的一个焦点
的一个焦点 与抛物线
与抛物线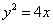 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为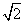 ,倾斜角为
,倾斜角为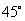 的直线
的直线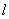 过点
过点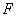 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)设椭圆的另一个焦点为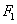 ,问抛物线
,问抛物线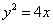 上是否存在一点
上是否存在一点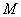 ,使得
,使得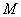 与
与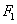 关于直线
关于直线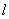 对称,若存在,求出点
对称,若存在,求出点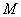 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(Ⅰ) ;(Ⅱ)抛物线
;(Ⅱ)抛物线 上存在一点
上存在一点 ,使得
,使得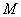 与
与 关于直线
关于直线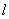 对称.
对称.
 (Ⅱ)∵ 倾斜角为
(Ⅱ)∵ 倾斜角为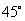 的直线
的直线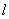 过点
过点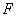 ,
,
∴ 直线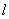 的方程为
的方程为 ,即
,即 ,………………………7分
,………………………7分
由(Ⅰ)知椭圆的另一个焦点为 ,设
,设 与
与 关于直线
关于直线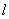 对称,则得
对称,则得 , ………………………………………9分
, ………………………………………9分
解得 ,即
,即 , ………………………………………11分
, ………………………………………11分
又 满足
满足 ,故点
,故点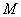 在抛物线上。所以抛物线
在抛物线上。所以抛物线 上存在一点
上存在一点 ,使得
,使得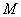 与
与 关于直线
关于直线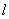 对称。 ………………………………13分
对称。 ………………………………13分
考点:直线与圆锥曲线的综合问题;椭圆的标准方程;抛物线的简单性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到达火车站的人进行调查,调查结果如下:
| 所用时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| 选择L1的人数 | 6 | 12 | 18 | 12 | 12 |
| 选择L2的人数 | 0 | 4 | 16 | 16 | 4 |
(1)试估计40分钟内不能赶到火车站的概率;
(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽最大可能 在允许的时间内赶到火车
在允许的时间内赶到火车 站,试通过计算说明,他们应如何选择各自的路径.
站,试通过计算说明,他们应如何选择各自的路径.

 表示不超过
表示不超过 的最大整数,例如:[3.1]=3,[
的最大整数,例如:[3.1]=3,[ 2.6]=
2.6]= 是函数
是函数 导函数,设
导函数,设 ,则函数
,则函数 的值域是( )
的值域是( ) B.
B. C.
C. D.
D.
 ,则AB =____________
,则AB =____________ 
 ( )
( ) (B)
(B) (C)
(C) (D)
(D) 
 (
( 为虚数单位)为纯虚数,则实数
为虚数单位)为纯虚数,则实数 .
. 是方程
是方程 的解,
的解,  是方程
是方程 的解,函数
的解,函数 ,则 ( )
,则 ( ) B.
B.
 D.
D.
 .若
.若 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C、
C、 D、
D、