题目内容
已知函数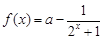
，
.
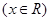（1）用定义证明：不论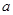
为何实数
在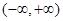
上为增函数；
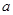（2）若为奇函数，求的值；
（3）在（2）的条件下，求在区间[1，5]上的最小值.
解: (1) 
的定义域为R, 任取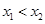
,
则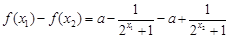
=
. 
,∴ 
.
∴
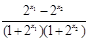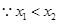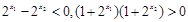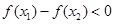，即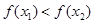
.
所以不论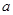为何实数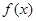
总为增函数.
(2) 
.
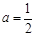(3)在区间
上的最小值为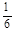
.
解析
练习册系列答案
相关题目
题目内容
已知函数，.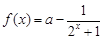
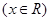（1）用定义证明：不论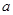为何实数在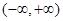上为增函数；
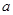（2）若为奇函数，求的值；
（3）在（2）的条件下，求在区间[1，5]上的最小值.
解: (1) 的定义域为R, 任取,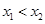
则=. ,∴ .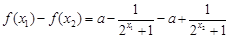
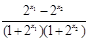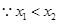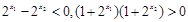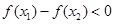∴，即.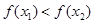
所以不论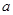为何实数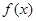总为增函数.
(2) .
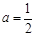(3)在区间上的最小值为.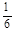
解析
在
上为增函数，求实数
的取值范围
时，求
上的最大值和最小值
，
恒成立
满足对一切
都有
,且
,
时有
.
的值;
上的单调性;
.
时，函数
取得最小值。
是定义在上的减函数，且
，求实数
的取值范围。
．
处的切线斜率为3，求实数m的值；
在[1，2]上是减函数，求实数m的取值范围． 
定义域为R，满足：①
；
，有
.
，
的值；
的值；
，使得不等式
对一切实数
成立.如果存在，求出常数
在区间
上的最大值和最小值.