题目内容
如图,在等腰梯形PDCB中,PB=3,DC=1,PD=BC=
,AD⊥PB,将△PAD沿AD折起,使平面PAD⊥平面ABCD.

(1)求证:PA⊥平面ABCD;
(2)求二面角P-DC-B的大小;
(3)若M是侧棱PB中点,求直线CM与平面PAB所成角的正弦值.
| 2 |

(1)求证:PA⊥平面ABCD;
(2)求二面角P-DC-B的大小;
(3)若M是侧棱PB中点,求直线CM与平面PAB所成角的正弦值.

证明:(1)在梯形PDCB中,PA⊥AD
又∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,PA?面PAD
∴PA⊥面ABCD
(2)由(1)得:PA⊥平面ABCD
又CD⊥AD,
∴CD⊥PD
∴∠PDA就是二面角P-DC-B的平面角
在Rt△PAD中,PA=AD=1,
∴∠PDA=45°
即二面角P-DC-B的大小为45°.
(3)作CE∥AD交AB于E点,连ME
∵AD⊥AB
∴CE⊥AB
∵PA⊥平面ABCD
∴面PAB⊥面ABCD
∴CE⊥面PAB,
∴∠CME是CM与平面PAB所成的角
∵CE=1,ME=
| 1 |
| 2 |
∴CM=
| ||
| 2 |
∴sin∠CME=
| CE |
| CM |
2
| ||
| 5 |

练习册系列答案
相关题目
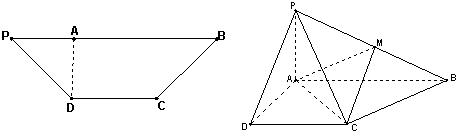
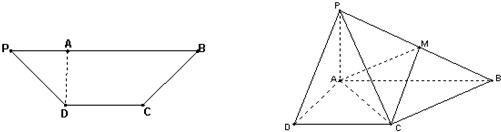
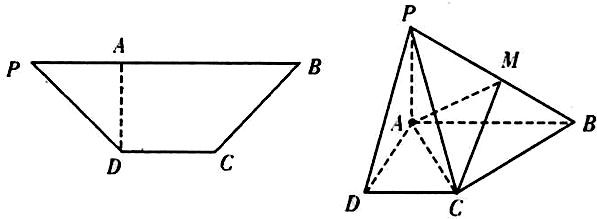
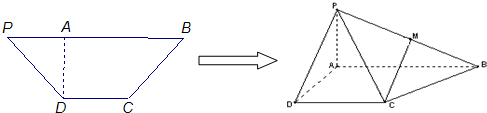
 (2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=
(2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=