题目内容
已知函数![]()
(I)讨论![]() 的单调性;
的单调性;
(II)若当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
解:(I)显然的定义域为(0,![]() )
)
![]()
令![]() ,则
,则![]()
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时, ![]()
∴![]() 在(0,3)上是单调递减函数,在(3,
在(0,3)上是单调递减函数,在(3,![]() )上是单调递增函数
)上是单调递增函数
∴当![]() 时,
时,
![]() 在(0,3)上是单调减函数,在(3,
在(0,3)上是单调减函数,在(3,![]() )上是单调增函数
)上是单调增函数
当![]() 时,
时,
![]() 在(0,3)上是单调增函数,在(3,
在(0,3)上是单调增函数,在(3,![]() )上是单调减函数
)上是单调减函数
(II)由上问可知,![]() 在[1,3)上是单调减函数,在(3,5
在[1,3)上是单调减函数,在(3,5![]() 上是单调增函数
上是单调增函数
∴![]() 在
在![]() 时取最小值,且最小值
时取最小值,且最小值![]() 。
。
又∵![]()
∴![]() 在
在![]() 时取最大值,且最大值
时取最大值,且最大值![]()
下面讨论![]() 的情况。
的情况。
①当![]() 时,在
时,在![]() 时
时![]() 取最小值,且最小值为
取最小值,且最小值为![]()
∵![]() 恒成立,∴
恒成立,∴![]() ,解得
,解得![]()
②当![]() 时,在
时,在![]() 时
时![]() 取最小值,且最小值为
取最小值,且最小值为![]()
由![]() 解得
解得![]() ,与
,与![]() 不符合,无解。
不符合,无解。
综合①②两种情况,知道所求![]() 的取值范围为
的取值范围为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
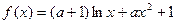
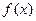 的单调性;
的单调性;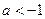 .如果对任意
.如果对任意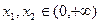 ,
,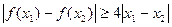 ,求
,求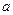 的取值范围。
的取值范围。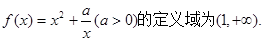
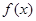 在其定义域上的单调性;
在其定义域上的单调性;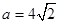 时,若关于x的方程
时,若关于x的方程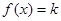 恰有两个不等实根,求实数k的取值范围。
恰有两个不等实根,求实数k的取值范围。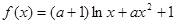
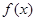 的单调性;
的单调性;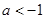 .如果对任意
.如果对任意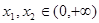 ,
,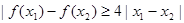 ,求
,求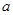 的取值范围。
的取值范围。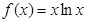
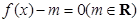 的解的个数;
的解的个数;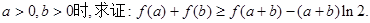
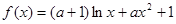
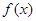 的单调性;
的单调性;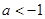 .如果对任意
.如果对任意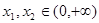 ,
,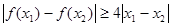 ,求
,求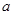 的取值范围。
的取值范围。