题目内容
已知F1,F2分别是椭圆 (a>b>0)的左、右焦点,半焦距为c,直线x=-
(a>b>0)的左、右焦点,半焦距为c,直线x=- 与x轴的交点为N,满足
与x轴的交点为N,满足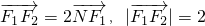 ,设A、B是上半椭圆上满足
,设A、B是上半椭圆上满足 的两点,其中
的两点,其中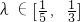 .
.
(1)求椭圆的方程及直线AB的斜率k的取值范围;
(2)过A、B两点分别作椭圆的切线,两切线相交于一点P,试问:点P是否恒在某定直线上运动,请说明理由.
解:(1)由于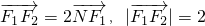 ,
,
∴
解得a2=2,b2=1,从而所求椭圆的方程为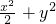 =1.
=1.
∵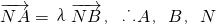 三点共线,而点N的坐标为(-2,0).
三点共线,而点N的坐标为(-2,0).
设直线AB的方程为y=k(x+2),其中k为直线AB的斜率,依条件知k≠0.
由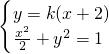 消去x得
消去x得 ,即
,即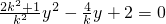 .
.
根据条件可知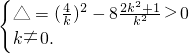 解得
解得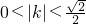 ,依题意取
,依题意取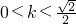 .
.
设A(x1,y1),B(x2,y2),则根据韦达定理,得 ,
,
又由 ,得(x1+2,y1)=λ(x2+2,y2)
,得(x1+2,y1)=λ(x2+2,y2)
,∴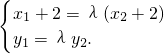 从而
从而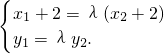
从而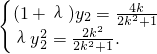 消去y2得
消去y2得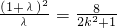 .
.
令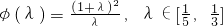 ,则
,则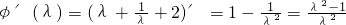 .
.
由于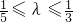 ,所以φ'(λ)<0.
,所以φ'(λ)<0.
∴φ(λ)是区间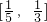 上的减函数,从而
上的减函数,从而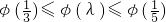 ,
,
即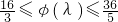 ,∴
,∴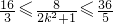 ,解得
,解得 ,而
,而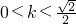 ,∴
,∴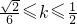 .
.
故直线AB的斜率的取值范围是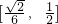 .
.
(2)设点P的坐标为(x0,y0),则可得切线PA的方程是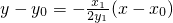 ,
,
而点A(x1,y1)在此切线上,有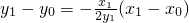 即x0x1+2y0y1=x12+2y12,
即x0x1+2y0y1=x12+2y12,
又∵A在椭圆上,∴有x0x1+2y0y=2,①同理可得x0x2+2y0y2=2.②
根据①和②可知直线AB的方程为,x0x+2y0y=2,而直线AB过定点N(-2,0),∴-2x0=2?x0=-1,
因此,点P恒在直线x=-1上运动.
分析:(1)依据题意联立方程求得a,b,则拖得方程可得.根据 判断出A,B,N三点共线,进而设出直线AB的方程,与椭圆的方程联立消去x,根据判别式大于0求得k的范围,设A(x1,y1),B(x2,y2),则根据韦达定理,可表示出y1+y2和y1y2,利用
判断出A,B,N三点共线,进而设出直线AB的方程,与椭圆的方程联立消去x,根据判别式大于0求得k的范围,设A(x1,y1),B(x2,y2),则根据韦达定理,可表示出y1+y2和y1y2,利用 求得(x1+2,y1)=λ(x2+2,y2),联立方程组消去y2,求得λ和k的关系,令
求得(x1+2,y1)=λ(x2+2,y2),联立方程组消去y2,求得λ和k的关系,令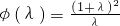 进而进行求导,推断函数的单调性,根据λ的范围求得k的范围.
进而进行求导,推断函数的单调性,根据λ的范围求得k的范围.
(2)设出P的坐标,进而求得PA的方程,把点A代入,同时代入椭圆的方程,推断出直线AB的方程,根据其过定点求得x0,进而推断出点P恒在直线x=-1上运动.
点评:本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线的综合问题是支撑圆锥曲线知识体系的重点内容,问题的解决具有入口宽、方法灵活多样等,而不同的解题途径其运算量繁简差别很大,故此类问题能有效地考查考生分析问题、解决问题的能力,平时应作为重点来复习训练.
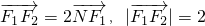 ,
,∴

解得a2=2,b2=1,从而所求椭圆的方程为
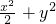 =1.
=1.∵
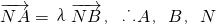 三点共线,而点N的坐标为(-2,0).
三点共线,而点N的坐标为(-2,0).设直线AB的方程为y=k(x+2),其中k为直线AB的斜率,依条件知k≠0.
由
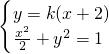 消去x得
消去x得 ,即
,即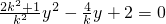 .
.根据条件可知
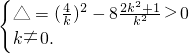 解得
解得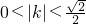 ,依题意取
,依题意取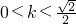 .
.设A(x1,y1),B(x2,y2),则根据韦达定理,得
 ,
,又由
 ,得(x1+2,y1)=λ(x2+2,y2)
,得(x1+2,y1)=λ(x2+2,y2),∴
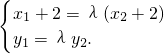 从而
从而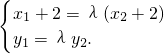
从而
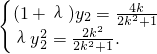 消去y2得
消去y2得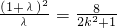 .
.令
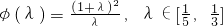 ,则
,则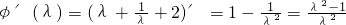 .
.由于
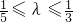 ,所以φ'(λ)<0.
,所以φ'(λ)<0.∴φ(λ)是区间
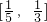 上的减函数,从而
上的减函数,从而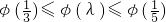 ,
,即
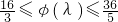 ,∴
,∴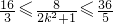 ,解得
,解得 ,而
,而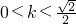 ,∴
,∴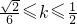 .
.故直线AB的斜率的取值范围是
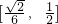 .
.(2)设点P的坐标为(x0,y0),则可得切线PA的方程是
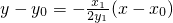 ,
,而点A(x1,y1)在此切线上,有
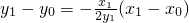 即x0x1+2y0y1=x12+2y12,
即x0x1+2y0y1=x12+2y12,又∵A在椭圆上,∴有x0x1+2y0y=2,①同理可得x0x2+2y0y2=2.②
根据①和②可知直线AB的方程为,x0x+2y0y=2,而直线AB过定点N(-2,0),∴-2x0=2?x0=-1,
因此,点P恒在直线x=-1上运动.
分析:(1)依据题意联立方程求得a,b,则拖得方程可得.根据
 判断出A,B,N三点共线,进而设出直线AB的方程,与椭圆的方程联立消去x,根据判别式大于0求得k的范围,设A(x1,y1),B(x2,y2),则根据韦达定理,可表示出y1+y2和y1y2,利用
判断出A,B,N三点共线,进而设出直线AB的方程,与椭圆的方程联立消去x,根据判别式大于0求得k的范围,设A(x1,y1),B(x2,y2),则根据韦达定理,可表示出y1+y2和y1y2,利用 求得(x1+2,y1)=λ(x2+2,y2),联立方程组消去y2,求得λ和k的关系,令
求得(x1+2,y1)=λ(x2+2,y2),联立方程组消去y2,求得λ和k的关系,令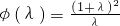 进而进行求导,推断函数的单调性,根据λ的范围求得k的范围.
进而进行求导,推断函数的单调性,根据λ的范围求得k的范围.(2)设出P的坐标,进而求得PA的方程,把点A代入,同时代入椭圆的方程,推断出直线AB的方程,根据其过定点求得x0,进而推断出点P恒在直线x=-1上运动.
点评:本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线的综合问题是支撑圆锥曲线知识体系的重点内容,问题的解决具有入口宽、方法灵活多样等,而不同的解题途径其运算量繁简差别很大,故此类问题能有效地考查考生分析问题、解决问题的能力,平时应作为重点来复习训练.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: