题目内容
如图的三角形数阵中，满足：（1）第1行的数为1；（2）第n（n≥2）行首尾两数均为n，其余的数都等于它肩上的两个数相加．则第n行（n≥2）中第2个数是| n2-n+2 |
| 2 |
| n2-n+2 |
| 2 |
分析：由三角形阵可知，上一行第二个数与下一行第二个数满足等式an+1=an+n，利用累加法可求．
解答：解：设第一行的第二个数为a1=1，
由此可得上一行第二个数与下一行第二个数满足等式an+1=an+n，
即a2-a1=1，a3-a2=2，a4-a3=3，…an-1-an-2=n-2，an-an-1=n-1，
∴an=（an-an-1）+（an-1-an-2）+…+（a4-a3）+（a3-a2）+（a2-a1）+a1=（n-1）+（n-2）+…+3+2+1+1=
+1=
；
故答案为：
．
由此可得上一行第二个数与下一行第二个数满足等式an+1=an+n，
即a2-a1=1，a3-a2=2，a4-a3=3，…an-1-an-2=n-2，an-an-1=n-1，
∴an=（an-an-1）+（an-1-an-2）+…+（a4-a3）+（a3-a2）+（a2-a1）+a1=（n-1）+（n-2）+…+3+2+1+1=
| (n-1)•n |
| 2 |
| n2-n+2 |
| 2 |
故答案为：
| n2-n+2 |
| 2 |
点评：本题数列的函数特性、简单的合情推理，属基础题，根据三角形阵寻找规律是解决该题的关键所在．
练习册系列答案
相关题目
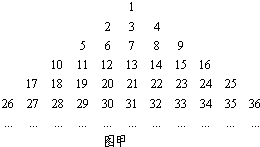把正整数排列成如图甲三角形数阵，然后擦去第偶行数中的奇数和第奇数行中的偶数，得到如图乙的三角形数阵，设aij位于图乙三角形数表中从上往下数第i行第j列的数，若amn=2011，则实数对（m，n）为
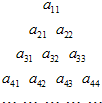将如图所示的三角形数阵中所有的数按从上至下、从左至右的顺序排列成数列a11，a21，a22，a31，a32，…．若所得数列构成一个等差数列，且a11=2，a33=12，则
