题目内容
函数f（x）对任意正整数a，b满足条件f（a+b）=f（a）•f（b），且f（1）=2．则
+
+
+…+
的值为
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2010) |
| f(2009) |
2010
2010
．分析：根据题意，在f（a+b）=f（a）•f（b）中，令b=1可得，f（a+1）=f（a）•f（1），可以变形为
=f（1），结合题意可得
=2，代入
+
+
+…+
中可得答案．
| f(a+1) |
| f(a) |
| f(a+1) |
| f(a) |
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2010) |
| f(2009) |
解答：解：在f（a+b）=f（a）•f（b）中，令b=1可得，f（a+1）=f（a）•f（1），即
=f（1），
又由f（1）=2，则
=2，
即
=
=
=…=
=2，
则
+
+
+…+
=2+2+…+2=2×1005=2010；
故答案为：2010．
| f(a+1) |
| f(a) |
又由f（1）=2，则
| f(a+1) |
| f(a) |
即
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2010) |
| f(2009) |
则
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2010) |
| f(2009) |
故答案为：2010．
点评：本题考查抽象函数的应用，解此类问题的一般方法是赋值法，注意结合题意，选择合适的值．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
函数f（x）对任意正整数a、b满足条件f（a+b）=f（a）f（b），且f（1）=2，则
+
+
+…+
的值是（ ）
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2008) |
| f(2007) |
| A、2007 | B、2008 |
| C、2006 | D、2005 |
+
+
+…+
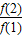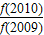的值为 ．