题目内容
设a1≈| 2 |
| 1 |
| 1+a1 |
(1)证明
| 2 |
(2)求a1、a2中哪一个更接近于
| 2 |
(3)你能设计一个比a2更接近于
| 2 |
分析:(1)中,只要证明(
-a1)(
-a2)< 0即可.
(2)用|
-a|来刻画a与
的接近程度.
(3)由前两题的规律,找出相应满足条件的数.
| 2 |
| 2 |
(2)用|
| 2 |
| 2 |
(3)由前两题的规律,找出相应满足条件的数.
解答:(1)证明:(
-a1)(
-a2)=(
-a1)•(
-1-
)=
<0.
∴
介于a1、a2之间.
(2)解:|
-a2|=|
-1-
|
=|
|
=
|
-a1|<|
-a1|.
∴a2比a1更接近于
.
(3)解:令a3=1+
,
则a3比a2更接近于
.
由(2)知|
-a3|=
|
-a2|<|
-a2|.
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 1+a1 |
(1-
| ||||
| 1+a1 |
∴
| 2 |
(2)解:|
| 2 |
| 2 |
| 1 |
| 1+a1 |
=|
(1-
| ||||
| 1+a1 |
=
| ||
| 1+a1 |
| 2 |
| 2 |
∴a2比a1更接近于
| 2 |
(3)解:令a3=1+
| 1 |
| 1+a2 |
则a3比a2更接近于
| 2 |
由(2)知|
| 2 |
| ||
| 1+a2 |
| 2 |
| 2 |
点评:本题中,对于大小比较时,主要是作差的方法.第三小问的处理,是在前两问的基础上观察得到的规律.

练习册系列答案
相关题目
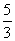 ,an+2=
,an+2=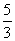 an+1-
an+1- an(n=1,2,…),
an(n=1,2,…),