题目内容
若非零函数f(x)对任意实数a,b均有f(a+b)=f(a)·f(b),且当x<0时,f(x)>1。
(1)求证:f(x)>0;
(2)求证:f(x)为减函数;
(3)当 时,解不等式
时,解不等式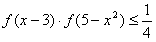 。
。
(1)求证:f(x)>0;
(2)求证:f(x)为减函数;
(3)当
 时,解不等式
时,解不等式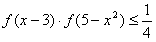 。
。 解:(1) ,
,
又若f(x0)=0,
则f(x)=f(x-x0+x0)=f(x-x0)f(x0)=0与已经矛盾,故 f(x)>0。
(2)设 ,则
,则 ,
,
又∵f(x)为非零函数,
∴

 ,
,
∴f(x)为减函数。
(3)由 ,由(1)
,由(1) ,
,
原不等式转化为 ,
,
结合(2)得: ,
,
故不等式的解集为 。
。
 ,
,又若f(x0)=0,
则f(x)=f(x-x0+x0)=f(x-x0)f(x0)=0与已经矛盾,故 f(x)>0。
(2)设
 ,则
,则 ,
,又∵f(x)为非零函数,
∴


 ,
,∴f(x)为减函数。
(3)由
 ,由(1)
,由(1) ,
,原不等式转化为
 ,
,结合(2)得:
 ,
,故不等式的解集为
 。
。 
练习册系列答案
相关题目