题目内容
线段
过
轴正半轴上一定点
，两端点
、
到轴的距离之积为
，
为坐标原点，以轴为对称轴，经过、、三点作抛物线.
（1）求这条抛物线方程；
（2）若
求
的最大值.
（1）
（2）
解析:
（1）可设抛物线方程为
，
设直线
的方程为
……………2分
联立这两个方程组消去
得，
………4分
设
，由已知得
注意到
，所以
，
又
所以
因为
所以
………………6分
（2）因为
所以
，
即
又
，
所以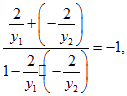
整理得
…………………8分
因为
所以
，从而
即
所以
即
因此
…………………………10分
又当
轴时，
，所以
即
于是
且
，解之不等式组得到
故
的最大值是…………12分
练习册系列答案
阅读快车系列答案
相关题目
轴正半轴上，S是抛物线C上任意一点，T是直线L上任意一点，若|ST|的最小值为d>0时,点S的横坐标为2. 
作直线与抛物线交于
两点，点
是点
关于原点的对称点.设点
所成的比为
，
；
（本小题满分12分）线段
过
轴正半轴上一定点
，两端点
、
到
，
为坐标原点，以
的最大值.