题目内容

4．如图，直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点，则|AB|+|CD|=（　　）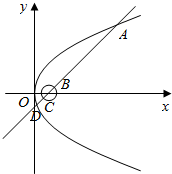
A．13B．14C．15D．16

分析 化圆的方程为（x-2）2+y2=1，抛物线y2=8x的焦点为（2，0），直线y=x-2过（2，0）点，则|AB|+|CD|=|AD|-2，联立直线y=x-2与y2=8x可得x2-12x+4=0，由此能够推导出|AB|+|CD|=16-2=14．

解答 解：由x2+y2-4x+3=0，得（x-2）2+y2=1，
∵抛物线y2=8x的焦点为（2，0），∴直线y=x-2过（2，0）点，
则|AB|+|CD|=|AD|-2，
联立直线y=x-2与y2=8x，可得x2-12x+4=0，
设A（x1，y1），D（x2，y2），则x1+x2=12，
则有|AD|=（x1+x2）+4=16，
故|AB|+|CD|=16-2=14．
故选：B．

点评 本题考查圆锥曲线和直线 的综合运用，解题时要注意合理地进行等价转化，是中档题．

练习册系列答案
相关题目
10．（1）若f（x）+f（$\frac{x-1}{x}$）=1+x，求f（x）；
（2）若2f（x）+f（1-x）=1+x，求f（x）．
11．已知指数函数y=ax（a＞0，且a≠1）的图象经过点（1，3）．
（1）求函数的解析式；
（2）求当x=-1，0，2时的函数值；
（3）画出函数的图象；
（4）叙述函数的性质．
8．已知数列{an}的首项a1=1，?n∈N*，an+1=$\frac{2{a}_{n}}{2+{a}_{n}}$．
（1）求数列{an}的通项公式；
（2）求数列{$\frac{{a}_{n}}{n}$}的前n项和Sn；
（3）求证：?n∈N*，a12+a22+a32+…+an2＜3．
15．已知集合M={x|（x-a）（x2-ax+a-1）=0}中各元素之和为3，则实数a的值为2或$\frac{3}{2}$．
9．已知两个大小相等的共点力F1，F2，当他们的夹角为90°时，合力的大小为10N，则当他们的夹角是120°时，合力大小是$5\sqrt{2}$N．
16．某工厂生产某种产品，固定成本20000元，每生产一件产品成本增加100元，已知总收益R元（R指工厂售出产品的全部收入，它是成本与利润之和），是年产量Q（单位：件）的函数．满足关系式$R=\left\{\begin{array}{l}400Q-\frac{1}{2}{Q^2}\;\;\;（0≤Q≤400）\\ 80000\;\;\;\;\;\;\;\;\;\;\;\;\;\;（Q＞400）\end{array}\right.$，求该厂每年生产多少件产品，总利润最大，最大值是多少？
13．已知在△ABC中，sinA+cosA=$\frac{{\sqrt{5}}}{5}$
（Ⅰ）求sinA-cosA的值；
（Ⅱ）求$\frac{{5{{sin}^2}A+sin（A-\frac{π}{2}）cos（A+\frac{3π}{2}）-5{{cos}^2}A}}{sinAcosA}$的值．
14．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|，＜$\overrightarrow{c}-\overrightarrow{a}，\overrightarrow{c}-\overrightarrow{b}$＞=$\frac{2π}{3}$，则$\frac{|\overrightarrow{c}|}{|\overrightarrow{a}|}$的最大值为$\frac{2\sqrt{3}}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网