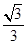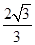题目内容
已知动圆C经过点(0,m) (m>0),且与直线y=-m相切,圆C被x轴截得弦长的最小值为1,记该圆的圆心的轨迹为E.
(Ⅰ)求曲线E的方程;
(Ⅱ)是否存在曲线C与曲线E的一个公共点,使它们在该点处有相同的切线?若存在,求出切线方程;若不存在,说明理由.
(Ⅰ)求曲线E的方程;
(Ⅱ)是否存在曲线C与曲线E的一个公共点,使它们在该点处有相同的切线?若存在,求出切线方程;若不存在,说明理由.
(Ⅰ)x2=2y;(Ⅱ)存在题设的公共点B,其坐标为(±2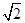 ,4),公切线方程为y=2
,4),公切线方程为y=2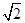 (x-2
(x-2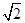 )+4或y=-2
)+4或y=-2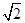 (x+2
(x+2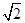 )+4,即y=±2
)+4,即y=±2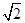 x-4.
x-4.
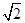 ,4),公切线方程为y=2
,4),公切线方程为y=2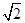 (x-2
(x-2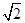 )+4或y=-2
)+4或y=-2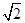 (x+2
(x+2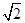 )+4,即y=±2
)+4,即y=±2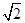 x-4.
x-4.试题分析:(Ⅰ)根据定义法确定轨迹为抛物线,然后借助圆C被x轴截得弦长的最小值为1求解参数m的值;(Ⅱ)假设存在题设的公共点B(b,
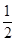 b2).利用圆的切线性质,以及利用导数的几何意义求解抛物线的切线方程的斜率建立等量关系,求解b的值进行论证.
b2).利用圆的切线性质,以及利用导数的几何意义求解抛物线的切线方程的斜率建立等量关系,求解b的值进行论证.试题解析:(Ⅰ)依题意,曲线E是以(0,m)为焦点,以y=-m为准线的抛物线.
曲线E的方程为x2=4my. 2分
设动圆圆心为A(a,
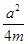 ),则圆C方程为(x-a)2+(y-
),则圆C方程为(x-a)2+(y-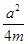 )2=(
)2=(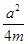 +m)2,
+m)2,令y=0,得(x-a)2=
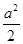 +m2.
+m2.当a=0时,圆C被x轴截得弦长取得最小值2m,于是m=
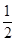 ,
,故曲线E的方程为x2=2y. 5分
(Ⅱ)假设存在题设的公共点B(b,
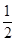 b2).
b2).圆C方程为(x-a)2+(y-
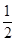 a2)2=(
a2)2=(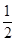 a2+
a2+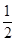 )2,
)2,将点B坐标代入上式,并整理,得(b-a)2[1+
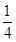 (a+b)2]=
(a+b)2]=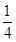 (a2+1)2.① 7分
(a2+1)2.① 7分对y=
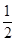 x2求导,得y¢=x,则曲线E在点B处的切线斜率为b.
x2求导,得y¢=x,则曲线E在点B处的切线斜率为b.又直线AB的斜率k=
 =
=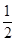 (a+b).
(a+b).由圆切线的性质,有
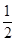 (a+b)b=-1. ② 8分
(a+b)b=-1. ② 8分由①和②得b2(b2-8)=0.
显然b≠0,则b=±2
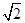 . 9分
. 9分所以存在题设的公共点B,其坐标为(±2
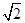 ,4),公切线方程为
,4),公切线方程为y=2
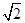 (x-2
(x-2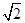 )+4或y=-2
)+4或y=-2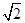 (x+2
(x+2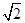 )+4,即y=±2
)+4,即y=±2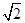 x-4. 12分
x-4. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的焦点坐标是( )
的焦点坐标是( )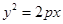 的焦点
的焦点 与双曲线
与双曲线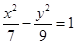 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与 轴的交点为
轴的交点为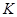 ,点
,点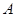 在抛物线上且
在抛物线上且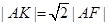 ,则△
,则△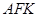 的面积为( )
的面积为( ) ,直线
,直线 过抛物线
过抛物线 的焦点,且与
的焦点,且与 两点,若
两点,若 为
为 的面积为
的面积为 ,则
,则 ( )
( )



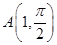 ,点
,点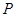 是曲线
是曲线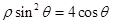 上任意一点,设点
上任意一点,设点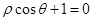 的距离为
的距离为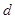 ,则
,则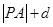 的最小值为 .
的最小值为 .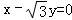 的距离是( )
的距离是( )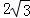
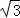
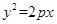 的焦点与
的焦点与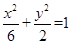 的左焦点重合,则
的左焦点重合,则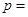 ( )
( )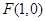 是抛物线
是抛物线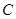 :
: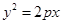 的焦点,则
的焦点,则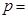 _______.
_______. 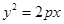 (
(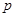 >
> )的焦点为
)的焦点为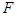 ,已知点
,已知点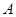 、
、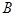 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足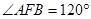 .过弦
.过弦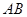 的中点
的中点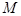 作抛物线准线的垂线
作抛物线准线的垂线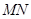 ,垂足为
,垂足为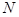 ,则
,则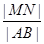 的最大值为 ( )
的最大值为 ( )