题目内容
已知函数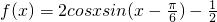 ].
].
(Ⅰ)求函数f(x)的最小值和最小正周期;
(Ⅱ)设△ABC的内角A、B、C的对边分别为a、b、c且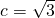 ,角C满足f(C)=0,若sinB=2sinA,求a、b的值.
,角C满足f(C)=0,若sinB=2sinA,求a、b的值.
解:(Ⅰ)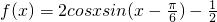 =
= sinxcosx-cos2x-
sinxcosx-cos2x- =
=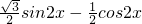 -1
-1
=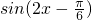 -1
-1
∴f(x)的最小值是-2,最小正周期为T= =π;
=π;
(Ⅱ)f(C)= -1=0,则
-1=0,则 =1
=1
∵0<C<π,∴C=
∵sinB=2sinA,∴由正弦定理可得b=2a①
∵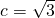 ,∴由余弦定理可得c2=a2+b2-ab=3②
,∴由余弦定理可得c2=a2+b2-ab=3②
由①②可得a=1,b=2.
分析:(Ⅰ)先化简函数f(x),再求函数的最小值和最小正周期;
(Ⅱ)先求C,再利用余弦定理、正弦定理,建立方程,即可求a、b的值.
点评:本题考查三角函数的化简,三角函数的性质,考查余弦定理、正弦定理的运用,属于中档题.
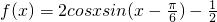 =
= sinxcosx-cos2x-
sinxcosx-cos2x- =
=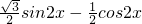 -1
-1=
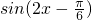 -1
-1∴f(x)的最小值是-2,最小正周期为T=
 =π;
=π;(Ⅱ)f(C)=
 -1=0,则
-1=0,则 =1
=1∵0<C<π,∴C=

∵sinB=2sinA,∴由正弦定理可得b=2a①
∵
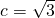 ,∴由余弦定理可得c2=a2+b2-ab=3②
,∴由余弦定理可得c2=a2+b2-ab=3②由①②可得a=1,b=2.
分析:(Ⅰ)先化简函数f(x),再求函数的最小值和最小正周期;
(Ⅱ)先求C,再利用余弦定理、正弦定理,建立方程,即可求a、b的值.
点评:本题考查三角函数的化简,三角函数的性质,考查余弦定理、正弦定理的运用,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目