题目内容

关于x的二次函数f(x)= x2-4x+1(0≤x≤1)的最大值为M，最小值为m，求M-m.

思路点拨：抛物线开口方向未知，顶点坐标与对称轴又都随a值而变化，唯一能知道的是当x=0时，f(x)=f(0)=1,即f(x)的图象过定点（0，1）只能将f(x)=x2-4x+1=(x-2a)2+1-4a,根据0≤x≤1,f(x)的最大值M,最小值m,顶点坐标为（2a,1-4a）,由顶点坐标位置分类讨论，根据图象求出M与m.

解：f(x)= x2-4x+1=(x-2a)2+1-4a（0≤x≤1）,顶点为（2a,1-4a）,f(0)=1,f(1)=-3.

当2a＜0,a＜0时，M-m=f(0)-f(1)=4-,

当0＜2a≤,0＜a≤时,M-m=f(1)-(1-4a)=4a+-4；

当＜2a≤1,＜a≤时，M-m=f(0)-(1-4a)=4a；

当2a＞1,a＞时，M-m=f(0)-f(1)=4-.

综上,M-m=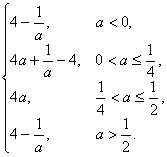

练习册系列答案
相关题目
已知关于x的二次函数f（x）=x2+（2t-1）x+1-2t，
（1）求证：对于任意t∈R，方程f（x）=1必有实数根；
（2）若
1
2
＜t＜
3
4
，求证：方程f（x）=0在区间(-1，  0)及(0，  
1
2
)上各有一个实数根．
13、关于x的二次函数f（x）=x2-2x-a在[1，3]最小值为2，则a为何值？
已知关于x的二次函数f（x）=ax2-8bx+1．
（1）设集合M={1，2，3}和N={-1，1，2，3，4，5}，从集合M中随机取一个数作为a，从N中随机取一个数作为b，求函数y=f（x）在区间[2，+∞）上是增函数的概率；
（2）设点（a，b）是区域
x+y-6≤0
x＞0
y＞0
内的随机点，求函数y=f（x）在区间[2，+∞）上是增函数的概率．
已知集合M={-1，1，3，5}和N={-1，1，2，4}．设关于x的二次函数f（x）=ax2-4bx+1（a，b∈R）．
（Ⅰ）若b=1时，从集合M取一个数作为a的值，求方程f（x）=0有解的概率；
（Ⅱ）若从集合M和N中各取一个数作为a和b的值，求函数y=f（x）在区间[1，+∞）上是增函数的概率．
（2011•顺义区一模）已知关于x的二次函数f（x）=ax2-4bx+1，其中a，b满足
a+b-6≤0
a＞0
b＞0
则函数y=f（x）在区间[1，+∞）上是增函数的概率为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网