Question

19．从某学校高三年级800名学生中随机抽取50名测量身高，据测量，被抽取学生的身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，如图是按上述分组方法得到的条形图．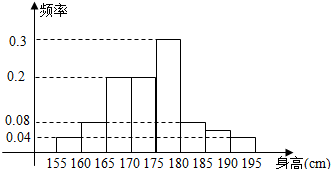

（1）根据已知条件填写下面表格：

组别	1	2	3	4	5	6	7	8
频数

（2）估计这所学校高三年级800名学生中身高在175cm以上（含175cm）的人数；
（3）在样本中，若第二组有1人为男生，其余为女生，第七组有1人为女生，其余为男生，在第二组和第七组中各选一名同学组成实验小组，问：实验小组中恰为同性别学生的概率是多少？

Answer 1

分析 （1）由频率分布直方图分析可得各数据段的频率，再由频率与频数的关系，可得频数．
（2）求出这所学校高三年级800名学生中身高在175cm以上（含1175cm）的频率，即得频数
（3）第二组四人记为a、b、c、d，其中a为男生，b、c、d为女生，第七组三人记为1、2、3，其中1、2为男生，3为女生，列出基本事件，根据概率公式计算即可．

解答 解：（1）由条形图得第七组频率为.1-（0.04×2+0.08×2+0.2×2+0.3）=0.06，∴0.06×50=3人∴第七组的人数为3人．（1分）

组别	1	2	3	4	5	6	7	8
频数	2	4	10	10	15	4	3	2

（4分）
（2）由条形图得前四组频率为0.04+0.08+0.2+0.2=0.52，后四组频率为1-0.52=0.48．估计这所学校高三年级身高在175cm以上（含175cm）的人数800×0.48=384（人）．（8分）
（3）第二组四人记为a、b、c、d，其中a为男生，b、c、d为女生，第七组三人记为1、2、3，其中1、2为男生，3为女生，基本事件列表如下：

	a	b	c	d
1	1a	1b	1c	1d
2	2a	2b	2c	2d
3	3a	3b	3c	3d

所以基本事件有12个，恰为一男一女的事件有1b，1c，1d，2b，2c，2d，3a共7个，因此实验小组中，恰为两男或两女的概率是$p=1-\frac{7}{12}$=$\frac{5}{12}$．        （12分）

点评 本题考查了古典概型概率计算及频率分布直方图的应用，关键是正确分析频率分布直方图的数据信息，准确计算．