题目内容
(16分)已知函数![]()
(1)判断函数![]() 的对称性和奇偶性;
的对称性和奇偶性;
(2)当![]() 时,求使
时,求使![]() 成立的
成立的![]() 的集合;
的集合;
(3)若![]() ,记
,记![]() ,试问
,试问![]() 在
在![]() 是否存在最大值,若存在求
是否存在最大值,若存在求![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
(16分)
解:(1)由函数![]() 可知,
可知,
函数![]() 的图象关于直线
的图象关于直线![]() 对称 …………………………3分
对称 …………………………3分
当![]() 时,函数
时,函数![]() 是一个偶函数;当
是一个偶函数;当![]() 时,取特值:
时,取特值:![]() ,故函数
,故函数![]() 是非奇非偶函数.…6分
是非奇非偶函数.…6分
(2)由题意得![]() ,得
,得![]() 或
或![]() ;
;
因此得![]() 或
或![]() 或
或![]() ,
,
故所求的集合为![]() . ……………………………11分
. ……………………………11分
(3)对于![]() ,
,![]()
若![]() ,
,![]() 在区间
在区间![]() 上递增,无最大值;
上递增,无最大值;
若![]() ,
,![]() 有最大值1
有最大值1
若![]() ,
,![]() 在区间
在区间![]() 上递增,在
上递增,在![]() 上递减,
上递减,![]() 有最大值
有最大值![]() ;
;
综上所述得,当![]() 时,
时,![]() 有最大值. …………………………16分
有最大值. …………………………16分

练习册系列答案
相关题目
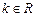 ,函数
,函数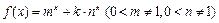 .
.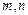 满足
满足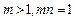 ,函数
,函数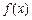 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的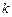
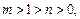 判断函数
判断函数 ,
,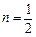 ,且
,且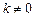 ,求函数
,求函数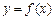 的对称轴或对称中心.
的对称轴或对称中心.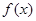 满足满足
满足满足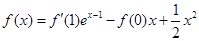 ;
;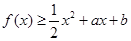 ,求
,求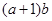 的最大值.
的最大值.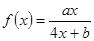
 ,在
,在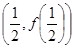 处的
处的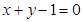 .
.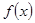 的解析式;
的解析式;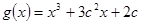
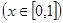 ,若对任意
,若对任意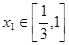 ,总存在
,总存在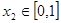 ,使得
,使得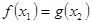 成立,求实数
成立,求实数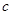 的取值范围.
的取值范围.