题目内容
(本题16分)已知函数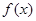 满足满足
满足满足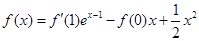 ;
;
(1)求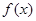 的解析式及单调区间;
的解析式及单调区间;
(2)若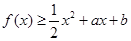 ,求
,求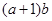 的最大值.
的最大值.
【答案】
(1)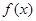 的解析式为
的解析式为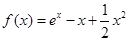 ,单调递增区间为
,单调递增区间为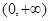 ,单调递减区间为
,单调递减区间为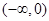 ;(2)
;(2)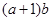 的最大值为
的最大值为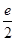
【解析】利用导数与函数单调性的关系求解单调区间以及利用导数求解函数的最值求解。
试题分析:
(1)
令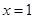 得:
得: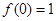
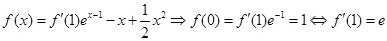
得: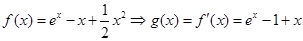
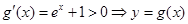 在
在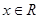 上单调递增
上单调递增
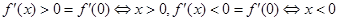
得: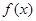 的解析式为
的解析式为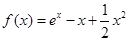
且单调递增区间为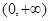 ,单调递减区间为
,单调递减区间为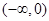 ……………8分
……………8分
(2)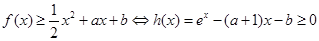 得
得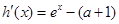
①当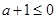 时,
时,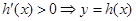 在
在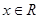 上单调递增
上单调递增
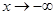 时,
时,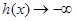 与
与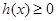 矛盾
矛盾
②当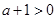 时,
时,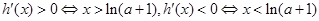
得:当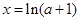 时,
时,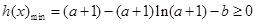
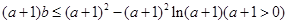
令 ;则
;则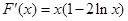
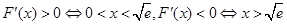
当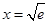 时,
时,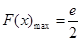
当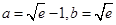 时,
时,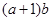 的最大值为
的最大值为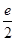 ………………………16分
………………………16分
考点:本题主要考查了利用导数与函数单调性的关系求解单调区间以及利用导数求解函数的最值等知识,综合考查了学生的运算求解能力和推理论证能力以及转化意识。
点评:解决此题的关键是熟练掌握利用导数与函数单调性的关系求解单调区间以及利用导数求解函数的最值的方法,以及较强的逻辑推理、运算求解及转化能力,难度很大。

练习册系列答案
相关题目
 是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x
的集合). ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明; (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值.