Question

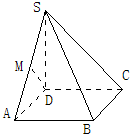
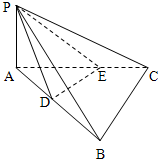
如图，在三棱锥P-ABC中，PA⊥平面ABC，AB=BC=CA=2PA，D、E分别是棱AB，AC上的动点，且AD=CE，连接DE，当三棱锥P-ADE体积最大时，平面PDE和平面PBC所成二面角的余弦值为（　　）

A． 1 2

B． 3 2

C． 21 14

D． 5 7 14

Answer 1

由题意，设AB=BC=CA=2PA=2，AD=CE=t，则三棱锥P-ADE体积为

1

3

×

1

2

×t×(2-t)×

3

2

=

3

12

(-t2+2t)
=-

3

12

(t-1)2+

3

12

∴t=1时，三棱锥P-ADE体积最大，此时，D、E分别是棱AB，AC上的中点
取DE中点M，BC中点N，连接PM，MN，PN，则
∵DE∥BC，PM⊥DE，PN⊥BC
∴∠MPN为平面PDE和平面PBC所成二面角，
在△MNP中，PM=

7

2

，MN=

3

2

，PN=2，
∴cos∠MPN=

PM2+PN2-MN2

2PM•PN

=

7 4 +4- 3 4

2• 7 2 •2

=

5 7

14

故选D．