题目内容
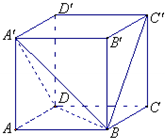
如图，直四棱柱ABCD-A1B1C1D1的高为3，底面是边长为4且∠DAB=60°的菱形，AC∩BD=O，A1C1∩B1D1=O1，则二面角O1-BC-D的大小为______．
作OF⊥BC，连接O1F，O1O．
∵O1O⊥平面ABCD，∴BC⊥O1F．
∴∠O1FO是二面角O1-BC-D的平面角．
在Rt△OBF中，∵BC=4，∠OBF=60°，
∴OF=
．
在Rt△O1OF中，tan∠O1FO=
=
=
．
∴∠O1FO=60°．
∴二面角O1-BC-D的大小为60°．
故答案为60°．
∵O1O⊥平面ABCD，∴BC⊥O1F．
∴∠O1FO是二面角O1-BC-D的平面角．
在Rt△OBF中，∵BC=4，∠OBF=60°，
∴OF=
| 3 |
在Rt△O1OF中，tan∠O1FO=
| O1O |
| OF |
| 3 | ||
|
| 3 |
∴∠O1FO=60°．
∴二面角O1-BC-D的大小为60°．
故答案为60°．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
