题目内容
5.对于曲线C所在的平面上的定点P,若存在以点P为顶点的角α,使得α≥∠APB对于曲线C上的任意两个不同的点A、B恒成立,则称角α为曲线C的“P点视角”,并称其中最小的“P点视角”为曲线C相对于点P的“P点确视角”.已知曲线C:x2+y2=2,相对于点P(2,0)的“P点确视角”的大小是$\frac{π}{2}$.分析 由题意,过P(2,0)的圆的切线的斜率分别为1,-1,即可求出相对于点P(2,0)的“P点确视角”的大小.
解答 解:由题意,曲线C:x2+y2=2表示以(0,0)为圆心,$\sqrt{2}$为半径的圆,
∴过P(2,0)的圆的切线的斜率分别为1,-1,
∴曲线C:x2+y2=2,相对于点P(2,0)的“P点确视角”的大小是$\frac{π}{2}$,
故答案为$\frac{π}{2}$.
点评 本题主要考查直线与圆的位置关系,求出过P(2,0)的圆的切线的斜率是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知函数f(x)=-x3+3x+m恰有两个零点,则实数m=( )
| A. | -2或2 | B. | -1或1 | C. | -1或-2 | D. | 1或2 |
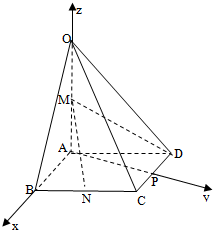 如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.
如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.