题目内容
已知函数f(x)=x|x+2|-2x-1
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)求不等式f(x)>0的解集.
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)求不等式f(x)>0的解集.
分析:(1)由f(x)=x|x+2|-2x-1,知当x≥-2时,f(x)=x(x+2)-2x-1=x2-1,当x<-2时,f(x)=x(-x-2)-2x-1=-x2-4x-1,由此能求出f(x)..
(2)由f(x)=
,知x=-2时,y=3;x=0时,y=-1;x=±1时,y=1.由此利用抛物线的对称性能求出f(x)的图象.
(3)由x2-1=0,得x=±1;由-x2-4x-1=0,得x=-2±
.结合图象,能求出不等式f(x)>0的解集.
(2)由f(x)=
|
(3)由x2-1=0,得x=±1;由-x2-4x-1=0,得x=-2±
| 3 |
解答:解:(1)∵f(x)=x|x+2|-2x-1,
∴当x≥-2时,f(x)=x(x+2)-2x-1=x2-1,
当x<-2时,f(x)=x(-x-2)-2x-1=-x2-4x-1,
∴f(x)=
.
(2)由f(x)=
,
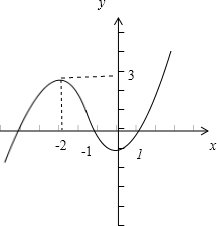
知x=-2时,y=3;x=0时,y=-1;x=±1时,y=1.
由此利用抛物线的对称性能求出f(x)的图象.
(3)由x2-1=0,得x=±1;
由-x2-4x-1=0,得x=-2±
.
∴结合图象,知不等式f(x)>0的解集为(-2-
,-1)∪(1,+∞).
∴当x≥-2时,f(x)=x(x+2)-2x-1=x2-1,
当x<-2时,f(x)=x(-x-2)-2x-1=-x2-4x-1,
∴f(x)=
|
(2)由f(x)=
|
知x=-2时,y=3;x=0时,y=-1;x=±1时,y=1.
由此利用抛物线的对称性能求出f(x)的图象.

(3)由x2-1=0,得x=±1;
由-x2-4x-1=0,得x=-2±
| 3 |
∴结合图象,知不等式f(x)>0的解集为(-2-
| 3 |
点评:本题考查函数解析式的求法,考查函数图象的作法,考查不等式的解法.解题时要认真审题,仔细解答.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|