题目内容
已知△ABC中，AB=2，BC=4，∠ABC=45°,BC在α内，且△ABC所在平面与平面α成30°角，则△ABC在α内的射影面积是（ ）A.
B.
C.
D.
答案:D
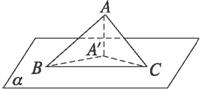
解析:如图所示，作AA′⊥α于点A′，连结A′B、A′C，则△A′BC为△ABC在平面α内的射影.
由公式S△=absinC可知
S△ABC=AB·BC·sin∠ABC=×2×4×sin45°=
.
又由公式
=cosθ,其中θ为这两个平面所成的角,
可知
=
=cos30°.
∴S△A′BC=S△ABC·cos30°=
.
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
（2009•辽宁）选修4-1：几何证明讲
定义平面向量的正弦积为
•
=|
||
|sin2θ，（其中θ为
、
的夹角），已知△ABC中，
•
=
•
，则此三角形一定是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| AB |
| BC |
| BC |
| CA |
| A、等腰三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |