题目内容
已知函数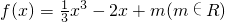 .
.
(1)求函数f(x)的单调区间;
(2)设a,b∈[-2,2],求证:|f(a)-f(b)|<5.
(1)解:求导函数,可得f′(x)=x2-2.
令f′(x)<0,可得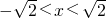 ;令f′(x)>0,可得
;令f′(x)>0,可得 或
或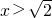 ,
,
∴f(x)单调递减区间为 ;f(x)单调递增为(-∞,-
;f(x)单调递增为(-∞,- ),(
),( ,+∞).
,+∞).
∴f(x)单调的单调递减区间为 ;单调的单调递增区间为
;单调的单调递增区间为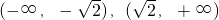 .
.
(2)证明:由(1)知函数f(x)在[-2,2]上的极大值为 ,极小值为
,极小值为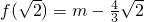 ;
;
又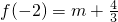 ,
,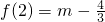 ,
,
∴f(x)在[-2,2]上的最大值 ,最小值为
,最小值为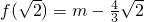 .
.
∴|f(a)-f(b)|≤|[f(x)]max-[f(b)]min|= .
.
分析:(1)求导函数,利用导数的正负,可得函数f(x)的单调区间;
(2)求出函数在[-2,2]上的最值,利用|f(a)-f(b)|≤|[f(x)]max-[f(b)]min|,即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查学生分析解决问题的能力,属于中档题.
令f′(x)<0,可得
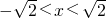 ;令f′(x)>0,可得
;令f′(x)>0,可得 或
或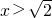 ,
,∴f(x)单调递减区间为
 ;f(x)单调递增为(-∞,-
;f(x)单调递增为(-∞,- ),(
),( ,+∞).
,+∞).∴f(x)单调的单调递减区间为
 ;单调的单调递增区间为
;单调的单调递增区间为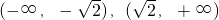 .
.(2)证明:由(1)知函数f(x)在[-2,2]上的极大值为
 ,极小值为
,极小值为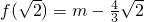 ;
;又
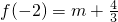 ,
,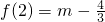 ,
,∴f(x)在[-2,2]上的最大值
 ,最小值为
,最小值为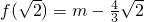 .
.∴|f(a)-f(b)|≤|[f(x)]max-[f(b)]min|=
 .
.分析:(1)求导函数,利用导数的正负,可得函数f(x)的单调区间;
(2)求出函数在[-2,2]上的最值,利用|f(a)-f(b)|≤|[f(x)]max-[f(b)]min|,即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.