Question

已知圆x²+y²-9x=0,与顶点在原点O,焦点在x轴上的抛物线交于A、B两点,△OAB的垂心恰为抛物线的焦点,求抛物线的方程.

Answer 1

解:依题意设所求抛物线方程为y²=2px(p＞0),焦点F(,0),A(x₀,y₀),B(x₀,-y₀),

则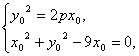

∴x₀²+(2p-9)x₀=0.                              ①

∵OA⊥BF,

∴k_OA·k_BF=-1.

∴

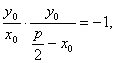
即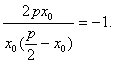

∴x₀=p.                                         ②

把②代入①得p=2.

∴所求抛物线方程为y²=4x.