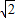题目内容
若lgx,lg(3x-2),lg(3x+2)成等差数列,则logx
的值为( )
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、不存在 |
分析:由已知中lgx,lg(3x-2),lg(3x+2)成等差数列,利用等差数列的性质和对数的运算性质,构造关于x的方程,解方程求出x值后,代入logx
,即可求出logx
的值.
| 2 |
| 2 |
解答:解:∵lgx,lg(3x-2),lg(3x+2)成等差数列
∴2lg(3x-2)=lgx+lg(3x+2)
则(3x-2)2=x•(3x+2)
即3x2-7x+2=0
解得:x=
,x=2
∵当x=
时,3x-2<0
故x=2,则logx
=log2
=
故选A
∴2lg(3x-2)=lgx+lg(3x+2)
则(3x-2)2=x•(3x+2)
即3x2-7x+2=0
解得:x=
| 1 |
| 3 |
∵当x=
| 1 |
| 3 |
故x=2,则logx
| 2 |
| 2 |
| 1 |
| 2 |
故选A
点评:本题考查的知识点是等差数列的性质及对数的运算性质,其中利用等差数列的性质和对数的运算性质,构造关于x的方程,是解答本题的关键.

练习册系列答案
相关题目
 的值为
的值为

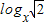 的值为( )
的值为( )