题目内容
已知数列{an}的前n项和Sn=aqn(a≠0,q≠1,q为非零常数),则数列{an}为 ( )A.等差数列 B.等比数列
C.既不是等差数列也不是等比数列 D.既是等差数列又是等比数列
思路分析:【常见误解】∵an+1=Sn+1-Sn=aqn+1-aqn=aqn(q-1),
an=Sn-Sn-1=aqn-1(q-1),∴![]() =q为常数.
=q为常数.
∴数列{an}为等比数列.
【错因分析】忽略了an=Sn-Sn-1中隐含n≥2的条件.
【正确解法】当n=1时,a1=S1=aq;
当n≥2时,an=Sn-Sn-1=aqn-1(q-1).
an+1=aqn(q-1),
∴![]() =q(n≥2)为常数,但
=q(n≥2)为常数,但![]() =q-1≠q,
=q-1≠q,
∴数列{an}从第二项起为等比数列.
答案:C

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
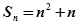 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________
 ,那么它的通项公式为an=_________
.
,那么它的通项公式为an=_________
. , 则数列的通项an=
, 则数列的通项an=