题目内容

若x、y∈R+，x+4y=20，则xy的最大值为
25
25
．
分析：利用基本不等式的性质即可求出．
解答：解：∵x、y∈R+，x+4y=20，
∴20≥2
4xy
，解得xy≤25，当且仅当x=4y=10，即x=10，y=
5
2
时取等号．
因此xy的最大值为25．
故答案为25．
点评：熟练掌握基本不等式的性质是解题的关键．
练习册系列答案
相关题目
若x、y∈R+，x+9y=12，则xy有最大值为
 
．
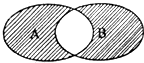精英家教网如图所示的韦恩图中，A，B是非空集合，定义集合A#B为阴影部分表示的集合．若x，y∈R，A={x|y=
2x-x2
}，B={y|y=3x，x＞0}，则A#B=（　　）
A、{x|0＜x＜2}
B、{x|1＜x≤2}
C、{x|0≤x≤1或x≥2}
D、{x|0≤x≤1或x＞2}
（2013•黄埔区一模）对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类P数对”．设函数f（x）的定义域为R+，且f（1）=3．
（1）若（1，1）是f（x）的一个“P数对”，求f（2n）（n∈N*）；
（2）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求f（x）在区间[1，2n）（n∈N*）上的最大值与最小值；
（3）若f（x）是增函数，且（2，-2）是f（x）的一个“类P数对”，试比较下列各组中两个式子的大小，并说明理由．
①f（2-n）与2-n+2（n∈N*）；
②f（x）与2x+2（x∈（0，1]）．
若x、y∈R+且
x
+
2y
≤a
x+y
恒成立，则a的最小值是（　　）
（2011•顺义区二模）对于定义域分别为M，N的函数y=f（x），y=g（x），规定：
函数h(x)=
f(x)•g(x)，当x∈M且x∈N
f(x)，当x∈M且x∉N
g(x)，当x∉M且x∈N

（1）若函数f(x)=
1
x+1
，g(x)=x2+2x+2，x∈R，求函数h（x）的取值集合；
（2）若f（x）=1，g（x）=x2+2x+2，设bn为曲线y=h（x）在点（an，h（an））处切线的斜率；而{an}是等差数列，公差为1（n∈N*），点P1为直线l：2x-y+2=0与x轴的交点，点Pn的坐标为（an，bn）．求证：
1
|P1P2|2
+
1
|P1P3|2
+…+
1
|P1Pn|2
＜
2
5
；
（3）若g（x）=f（x+α），其中α是常数，且α∈[0，2π]，请问，是否存在一个定义域为R的函数y=f（x）及一个α的值，使得h（x）=cosx，若存在请写出一个f（x）的解析式及一个α的值，若不存在请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网