题目内容
以下坐标给出的点中，在曲线
上的点是（ ）
|
分析：把所给的曲线的参数方程化为化为普通方程为 y2=1+x （-1≤x≤1），检验各个选项中的点的坐标是否满足此方程，从而得出结论．
解答：解：把曲线
消去参数θ，化为普通方程为 y2=1+x （-1≤x≤1），
结合所给的选项，只有C中的点在曲线上，
故选C．
|
结合所给的选项，只有C中的点在曲线上，
故选C．
点评：本题主要考查把参数方程化为普通方程的方法，判断点是否在已知曲线上，属于中档题．
练习册系列答案
相关题目
中，已知
，…，
是直线
上的
个点（
，
、
均为非零常数）.
成等差数列，求证：数列
也成等差数列；
是直线
上一点，且
，求
的值；
，我们称
是向量
，
，…，
的线性组合,
是该线性组合的系数数列.
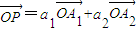，求a1+a2的值；
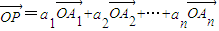，我们称
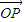是向量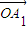
，
，…，
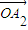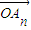的线性组合，{an}是该线性组合的系数数列．当
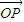是向量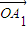
，
，…，
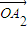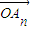的线性组合时，请参考以下线索：