题目内容
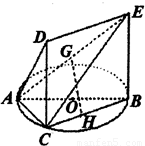
如图一简单几何体的一个面ABC内接于圆O,G,H分别上AE,BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.(1)求证:GH∥平面ACD;
(2)证明:平面ADE⊥平面ACD;
(3)若
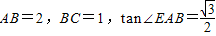 ,试求该几何体的体积V.
,试求该几何体的体积V.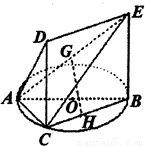
【答案】分析:(1)取AD的中点F,易证四边形CHGF为平行四边形,由线面平行的判断可得;(2)由DC⊥平面ABC,可得DC⊥BC,由直径所对的圆周角为直角可得BC⊥AC,易证DE⊥平面ACD,进而可得结论;(3)把几何体化为两个三棱锥来求即可的答案.
解答:证明:(1)取AD的中点F,连接GF,CF,在三角形ADE中,GF为中位线,
可得GF∥AD,且GF= AD,故GF=CH,且GF=CH,四边形CHGF为平行四边形,
AD,故GF=CH,且GF=CH,四边形CHGF为平行四边形,
故GH∥CF,由CF,GH分别在平面ACD内外,
故GH∥平面ACD;
(2)∵DC⊥平面ABC,∴DC⊥BC,由直径所对的圆周角为直角可得BC⊥AC,
由CD∩AC=C,故BC⊥平面ACD,即DE⊥平面ACD,又DE?平面ADE,
所以平面ADE⊥平面ACD;
(3)由题意可得:AC= =
= ,
, ,EB=
,EB= ,
,
V=VE-ACD+VE-ABC= S△ACD×DE+
S△ACD×DE+ S△ABC×EB
S△ABC×EB
= ×
×
 ×
× =1
=1
点评:本题为线面位置关系的综合应用,涉及线面平行,面面垂直和体积公式,属中档题.
解答:证明:(1)取AD的中点F,连接GF,CF,在三角形ADE中,GF为中位线,
可得GF∥AD,且GF=
 AD,故GF=CH,且GF=CH,四边形CHGF为平行四边形,
AD,故GF=CH,且GF=CH,四边形CHGF为平行四边形,故GH∥CF,由CF,GH分别在平面ACD内外,
故GH∥平面ACD;
(2)∵DC⊥平面ABC,∴DC⊥BC,由直径所对的圆周角为直角可得BC⊥AC,
由CD∩AC=C,故BC⊥平面ACD,即DE⊥平面ACD,又DE?平面ADE,
所以平面ADE⊥平面ACD;
(3)由题意可得:AC=
 =
= ,
, ,EB=
,EB= ,
,V=VE-ACD+VE-ABC=
 S△ACD×DE+
S△ACD×DE+ S△ABC×EB
S△ABC×EB=
 ×
×
 ×
× =1
=1点评:本题为线面位置关系的综合应用,涉及线面平行,面面垂直和体积公式,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图一简单几何体的一个面ABC内接于圆O,G,H分别是AE,BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图一简单几何体的一个面ABC内接于圆O,G,H分别是AE,BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.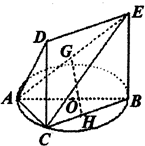 如图一简单几何体的一个面ABC内接于圆O,G,H分别上AE,BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图一简单几何体的一个面ABC内接于圆O,G,H分别上AE,BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.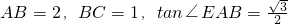 ,试求该几何体的体积V.
,试求该几何体的体积V. ,试求该几何体的体积V.
,试求该几何体的体积V.