题目内容
 如图,在斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2.底面ABC是边长为2的正三角形,M、N分别是AC和B1C1的中点.
如图,在斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2.底面ABC是边长为2的正三角形,M、N分别是AC和B1C1的中点.(Ⅰ)求证:MN∥侧面ABB1A1;
(Ⅱ)求MN与平面ABC所成的角的大小(用反三角函数表示).
分析:(Ⅰ)要证MN∥侧面ABB1A1,只需取A1B1的中点P,连接NP、AP,证明MN∥AP.MN?面ABB1A1,AP?面ABB1A1,即可.
(Ⅱ)通过MN与平面ABC所成的角和AP与平面ABC所成的角相等.连接PB,说明,∠PAB为直线PA与面ABC所成的角,通过tan∠PAB=
,求MN与平面ABC所成的角的大小(用反三角函数表示).
(Ⅱ)通过MN与平面ABC所成的角和AP与平面ABC所成的角相等.连接PB,说明,∠PAB为直线PA与面ABC所成的角,通过tan∠PAB=
| PB |
| AA1 |
解答: 解(Ⅰ)证明:取A1B1的中点P,连接NP、AP,
解(Ⅰ)证明:取A1B1的中点P,连接NP、AP,
则NP∥AM,NP=
A1C1=
AC=AM,
∴四边形AMNP为平行四边形,∴MN∥AP.
∵MN?面ABB1A1,AP?面ABB1A1,
∴MN∥侧面ABB1A1.
(Ⅱ)∵MN∥AP,∴MN与平面ABC所成的角和AP与平面ABC所成的角相等.连接PB,
∵四边形ABB1A1为菱形,且∠A1B1B=60°,∴PB⊥AB.
∵侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,
∴PB⊥底面ABC,∴∠PAB为直线PA与面ABC所成的角.
∵PB=
AA1=
,∴tan∠PAB=
,∴∠PAB=arctan
,
即MN与面ABC所成的角为arctan
.
 解(Ⅰ)证明:取A1B1的中点P,连接NP、AP,
解(Ⅰ)证明:取A1B1的中点P,连接NP、AP,则NP∥AM,NP=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形AMNP为平行四边形,∴MN∥AP.
∵MN?面ABB1A1,AP?面ABB1A1,
∴MN∥侧面ABB1A1.
(Ⅱ)∵MN∥AP,∴MN与平面ABC所成的角和AP与平面ABC所成的角相等.连接PB,
∵四边形ABB1A1为菱形,且∠A1B1B=60°,∴PB⊥AB.
∵侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,
∴PB⊥底面ABC,∴∠PAB为直线PA与面ABC所成的角.
∵PB=
| ||
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
即MN与面ABC所成的角为arctan
| ||
| 2 |
点评:本题考查直线与平面的平行,直线与平面所成角的求法,注意直线与平面平行的定理以及准确作出直线与平面所成的角,考查计算能力.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
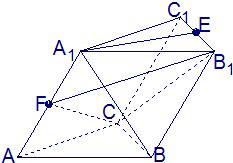 如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点
如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点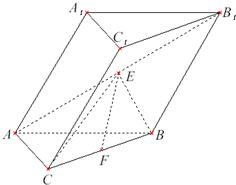 如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.  如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )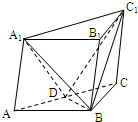 (2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点.
(2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点. (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=