题目内容
(满分12分)设函数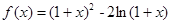 。
。
(Ⅰ)若在定义域内存在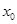 ,而使得不等式
,而使得不等式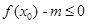 能成立,求实数
能成立,求实数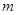 的最小值;
的最小值;
(Ⅱ)若函数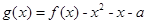 在区间
在区间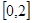 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。
(Ⅰ)实数 的最小值为
的最小值为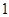 。(Ⅱ)
。(Ⅱ)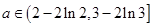 。
。
解析试题分析:(Ⅰ)要使得不等式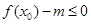 能成立,只需
能成立,只需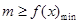 。
。
求导得: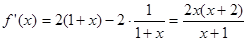 , ………3分
, ………3分
∵函数 的定义域为
的定义域为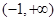 ,
,
当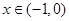 时,
时, ,∴函数
,∴函数 在区间
在区间 上是减函数;
上是减函数;
当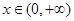 时,
时,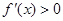 ,∴函数
,∴函数 在区间(0,+∞)上是增函数。
在区间(0,+∞)上是增函数。
∴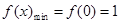 , ∴
, ∴ 。故实数
。故实数 的最小值为
的最小值为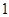 。 ………6分
。 ………6分
(Ⅱ)由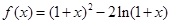 得:
得:
由题设可得:方程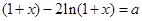 在区间
在区间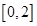 上恰有两个相异实根………8分
上恰有两个相异实根………8分
设 。∵
。∵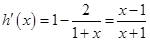 ,列表如下:
,列表如下:
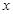
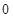
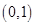
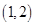
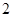


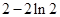

 ;
; 时,判断
时,判断 在定义域上的单调性;
在定义域上的单调性; 上的最小值.
上的最小值.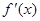 为f(x)的导函数,求证:
为f(x)的导函数,求证: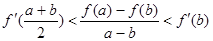
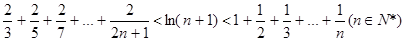
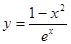 , 求
, 求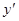
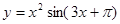 , 求
, 求 .
. ,求
,求 的最小值;
的最小值; ,讨论函数
,讨论函数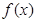 =
= (
( 为自然对数的底数),
为自然对数的底数), ,记
,记 .
. 为
为 的导函数,判断函数
的导函数,判断函数 的单调性,并加以证明;
的单调性,并加以证明; =0有两个零点,求实数
=0有两个零点,求实数 的取值范围.
的取值范围.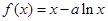 ,
,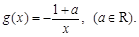
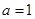 ,求函数
,求函数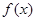 的极值;
的极值; ,求函数
,求函数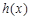 的单调区间;
的单调区间;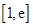 (
( )上存在一点
)上存在一点 ,使得
,使得
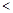
 成立,求
成立,求 的取值范围.
的取值范围. ..
..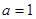 时,求
时,求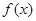 的单调区间;
的单调区间;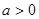 时,设
时,设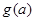 ,若
,若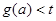 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.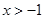 ,证明:
,证明: