题目内容
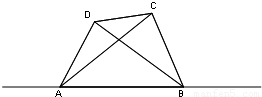
 一条河自西向东流淌,某人在河南岸A处看到河北岸两个目标C、D分别在东偏北45°和东偏北60°方向,此人向东走300米到达B处之后,再看C、D,则分别在西偏北75°和西偏北30°方向,求目标C、D之间的距离.
一条河自西向东流淌,某人在河南岸A处看到河北岸两个目标C、D分别在东偏北45°和东偏北60°方向,此人向东走300米到达B处之后,再看C、D,则分别在西偏北75°和西偏北30°方向,求目标C、D之间的距离.
解:△ABC中,∵∠DBA=30°,∠DAB=60°,∴∠ADB=90°,又 AB=300,
∴BD=300×sin60°=150 .
.
△ABC中,由正弦定理可得 =
= ,∴BC=100
,∴BC=100 .
.
△ABC中,由余弦定理可得 CD2= +3002-2×300×100
+3002-2×300×100 ×cos(75°-30°)=37500,
×cos(75°-30°)=37500,
∴CD=50 ,
,
即目标C、D之间的距离为50 .
.
分析:利用直角三角形中的边角关系求出 BD的值,△ABC中,由正弦定理可得 BC,△ABC中,由余弦定理可得 CD2 的值,
从而得到CD 的值.
点评:本题考查直角三角形中的边角关系,正弦定理、余弦定理的应用,求出 BD和BC的值,是解题的关键.
∴BD=300×sin60°=150
 .
.△ABC中,由正弦定理可得
 =
= ,∴BC=100
,∴BC=100 .
.△ABC中,由余弦定理可得 CD2=
 +3002-2×300×100
+3002-2×300×100 ×cos(75°-30°)=37500,
×cos(75°-30°)=37500,∴CD=50
 ,
,即目标C、D之间的距离为50
 .
.分析:利用直角三角形中的边角关系求出 BD的值,△ABC中,由正弦定理可得 BC,△ABC中,由余弦定理可得 CD2 的值,
从而得到CD 的值.
点评:本题考查直角三角形中的边角关系,正弦定理、余弦定理的应用,求出 BD和BC的值,是解题的关键.

练习册系列答案
相关题目
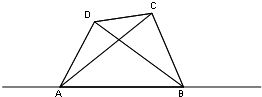
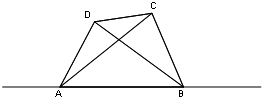 一条河自西向东流淌,某人在河南岸A处看到河北岸两个目标C、D分别在东偏北45°和东偏北60°方向,此人向东走300米到达B处之后,再看C、D,则分别在西偏北75°和西偏北30°方向,求目标C、D之间的距离.
一条河自西向东流淌,某人在河南岸A处看到河北岸两个目标C、D分别在东偏北45°和东偏北60°方向,此人向东走300米到达B处之后,再看C、D,则分别在西偏北75°和西偏北30°方向,求目标C、D之间的距离. 处看到河北岸
处看到河北岸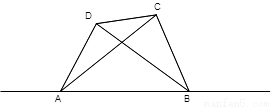
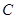 、
、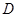 分别在东偏北
分别在东偏北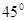 和东偏北
和东偏北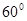 方向,此人
方向,此人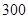 米到达
米到达 处之后,再看
处之后,再看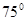 和西偏北
和西偏北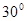 方向,求目标
方向,求目标