题目内容
已知向量a=(1,1),b=(1,-1),c=(A.2 B.3 C.4 D.16
答案:D
解析:由ma+nb=c,得(m,m)+(n,-n)=(![]() cosα,
cosα, ![]() sinα),
sinα),
即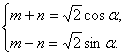
解得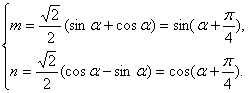
∴(m-3)2+n2=[sin(α+![]() )-3]2+cos2(α+
)-3]2+cos2(α+![]() )
)
=sin2(α+![]() )-6sin(α+
)-6sin(α+![]() )+9+cos2(α+
)+9+cos2(α+![]() )
)
=10-6sin(α+![]() ).
).
∴(m-3)2+n2的最大值为16.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
题目内容
已知向量a=(1,1),b=(1,-1),c=(A.2 B.3 C.4 D.16
答案:D
解析:由ma+nb=c,得(m,m)+(n,-n)=(![]() cosα,
cosα, ![]() sinα),
sinα),
即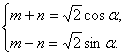
解得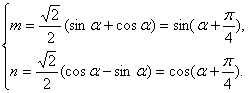
∴(m-3)2+n2=[sin(α+![]() )-3]2+cos2(α+
)-3]2+cos2(α+![]() )
)
=sin2(α+![]() )-6sin(α+
)-6sin(α+![]() )+9+cos2(α+
)+9+cos2(α+![]() )
)
=10-6sin(α+![]() ).
).
∴(m-3)2+n2的最大值为16.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案