若tanx=3.则1+sinxcosx的值为$\frac{13}{10}$．题目和参考答案——青夏教育精英家教网—

题目内容

5．若tanx=3，则1+sinxcosx的值为$\frac{13}{10}$．

分析由条件利用同角三角函数的基本关系，求得1+sinxcosx的值．

解答解：∵tanx=3，则1+sinxcosx=1+$\frac{sinxcosx}{{sin}^{2}x{+cos}^{2}x}$=1+$\frac{tanx}{{tan}^{2}x+1}$=1+$\frac{3}{9+1}$=$\frac{13}{10}$，
故答案为：$\frac{13}{10}$．

点评本题主要考查同角三角函数的基本关系，属于基础题．

练习册系列答案

16．已知i是虚数单位，则复数$\frac{1-2i}{1+2i}$=（　　）

A．

-$\frac{3}{5}$-$\frac{4}{5}$i

B．

-$\frac{3}{5}$+$\frac{4}{5}$i

C．

$\frac{3}{5}$-$\frac{4}{5}$i

D．

$\frac{3}{5}$+$\frac{4}{5}$i

13．已知f（x）=$\frac{1}{2}{x^2}+2x{f^'}（{2015}）+2015lnx$，则f′（2015）=（　　）

20．设函数f（x）=x²-1，对任意x∈[3，+∞），f（$\frac{x}{m}$）-4m²f（x）≤f（x-1）+4f（m）恒成立，则实数m的取值范围是$（-∞，-\frac{\sqrt{2}}{2}]∪[\frac{\sqrt{2}}{2}，+∞）$．

10．直线l₁经过点A（1，2）且与直线l₂：2x+2y-5=0垂直；
求：（1）直线l₁的方程；
（2）若已知圆O的方程为x²+y²=1，求直线l₁被圆截得的弦长．

17．设a∈R，函数f（x）=cosx（2asinx-cosx）+sin²x的图象的一条对称轴是直线$x=-\frac{π}{6}$．
（Ⅰ）求$f（-\frac{π}{3}）$的值和a的值；
（Ⅱ）求函数f（x）在$[\frac{π}{4}，\frac{π}{2}]$上的最大值和最小值．

14．等差数列{a_n}的公差d≠0，a₁=20，且a₃，a₇，a₉成等比数列．S_n为{a_n}的前n项和，则S₁₀的值为110．

15．

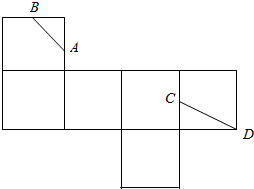如图是一个正方体的平面展开图，A，B，C均为所在棱的中点，D为正方体的顶点，若正方体的棱长为2，则在正方体中，封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$．

试题分类