题目内容
巳知函数f(x)=2sinxcos(
π+x)+
cosxsin(π+x)+sin(
+x) cosx
(1)求f(x)的值域;
(2)求f(x)的单调递增区间.
| 3 |
| 2 |
| 3 |
| π |
| 2 |
(1)求f(x)的值域;
(2)求f(x)的单调递增区间.
f(x)=2sin2x-
sinx•cosx+cos2x
=sin2x-
sinxcosx+1
=
+1
=
-sin(2x+
)
(1)∵sin(2x+
)∈[-1,1]
∴f(x)∈[
,
]
(2)由
+2kπ≤2x+
≤
+2kπ
可得,
+kπ≤x ≤
+kπ
即函数在[
+kπ,
+kπ] k∈Z单调递减
| 3 |
=sin2x-
| 3 |
=
1-cos2x-
| ||
| 2 |
=
| 3 |
| 2 |
| π |
| 6 |
(1)∵sin(2x+
| π |
| 6 |
∴f(x)∈[
| 1 |
| 2, |
| 5 |
| 2 |
(2)由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
可得,
| π |
| 6 |
| 2π |
| 3 |
即函数在[
| π |
| 6 |
| 2π |
| 3 |

练习册系列答案
相关题目
 .
. >f(
>f(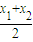 )成立;
)成立;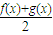 ,
, .
. .
.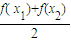 >f(
>f(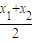 )成立;
)成立;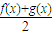 ,
, .
. .
. >f(
>f( )成立;
)成立; ,
, .
.