题目内容
巳知函数f(x)=2sinxcos(| 3 |
| 2 |
| 3 |
| π |
| 2 |
(1)求f(x)的值域;
(2)求f(x)的单调递增区间.
分析:利用同角平方关系及二倍角公式对函数化简可得f(x)=
-sin(2x+
)
(1)由正弦函数的性质可得-1≤sin(2x+
)≤1,代入可求函数的值域
(2) 由正弦函数的性质可得,由
+2kπ≤2x+
≤
+2kπ可得,
+kπ≤x ≤
+kπ即为所求的单调区间.
| 3 |
| 2 |
| π |
| 6 |
(1)由正弦函数的性质可得-1≤sin(2x+
| π |
| 6 |
(2) 由正弦函数的性质可得,由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
解答:解:f(x)=2sin2x-
sinx•cosx+cos2x
=sin2x-
sinxcosx+1
=
+1
=
-sin(2x+
)
(1)∵sin(2x+
)∈[-1,1]
∴f(x)∈[
,
]
(2)由
+2kπ≤2x+
≤
+2kπ
可得,
+kπ≤x ≤
+kπ
即函数在[
+kπ,
+kπ] k∈Z单调递减
| 3 |
=sin2x-
| 3 |
=
1-cos2x-
| ||
| 2 |
=
| 3 |
| 2 |
| π |
| 6 |
(1)∵sin(2x+
| π |
| 6 |
∴f(x)∈[
| 1 |
| 2, |
| 5 |
| 2 |
(2)由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
可得,
| π |
| 6 |
| 2π |
| 3 |
即函数在[
| π |
| 6 |
| 2π |
| 3 |
点评:本题主要考查了同角平方关系,二倍角公式在三角函数化简中应用,考查了函数y=Asin(ωx+φ)的值域及单调区间的求解,考查的是对基础知识、基本方法的掌握.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 .
. >f(
>f(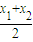 )成立;
)成立;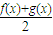 ,
, .
. .
.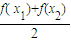 >f(
>f(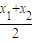 )成立;
)成立; ,
, .
. .
. >f(
>f( )成立;
)成立; ,
, .
.