Question

【题目】（本小题满分12分）

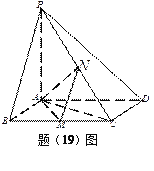
如图，已知四棱锥，底面为菱形，，

, 平面， 分别是的中点。

（1）证明： ；

（2）若为上的动点，与平面所成最大角

的正切值为，求二面角的余弦值。

Answer 1

【答案】（1）详见解析（2）

【解析】试题分析：(1)由已知条件推导出， ，由线面垂直得，由此证明

(2)设为上任意一点，连接、，由平面，得为与平面所成的角，过作于，连接，由已知条件得为二面角的平面角，由此求出二面角的余弦值.

试题解析：(1)证明：由四边形为菱形， ，可得为正三角形。

因为为BC的中点，所以,又,因此，

因为， 平面，所以，

而，所以

（2）设为上任意一点，连接、

由（1）知，

则为与平面所成的角，在中， ,

所以当最短时， 最大，即当时， 最大，

此时,此时，又，

所以 =45，于是

因为平面， 平面，所以平面平面，

过作于，则由面面垂直的性质定理可知: 平面,

所以，过过作于，连接， 平面，

所以,则为二面角的平面角，

在中， ，

又是的中点， ,

且

在中， ，

又=,

在中， ==

即二面角的余弦值为