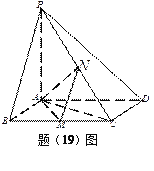
题目内容
【题目】在三棱锥![]() 中,
中, ![]() 和
和![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)见解析(3)![]() .
.
【解析】试题分析:(1)欲证OD∥平面PAC,根据直线与平面平行的判定定理可知只需证OD与平面PAC内一直线平行,而OD∥PA,PA平面PAC,OD平面PAC,满足定理条件; (2)欲证平面PAB⊥平面ABC,根据面面垂直的判定定理可知在平面PAB内一直线与平面ABC垂直,而根据题意可得PO⊥平面ABC;
(3)根据OP垂直平面ABC得到OP为三棱锥P-ABC的高,根据三棱锥的体积公式可求出三棱锥P-ABC的体积.又因为D为PB中点,所以高是PO的一半.
试题解析:(1)∵![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)连接![]() ,∵
,∵![]() 为
为![]() 中点,
中点, ![]() ,
,
∴![]() .
.
同理, ![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() .
.
(3)由(2)可知![]() 平面
平面![]() ,
,
∴![]() 为三棱锥
为三棱锥![]() 的高,且
的高,且![]() .
.
∴![]() .
.

练习册系列答案
相关题目