题目内容
已知数列{an}中,a1=1,且Sn=
思路分析:已知条件是一个关于Sn的递推式,可以先求出Sn,然后求an.
解:由Sn=∴{![]() }是首项为
}是首项为![]() =
=![]() =1,公差为2的等差数列.∴
=1,公差为2的等差数列.∴![]() =1+(n-1)×2=2n-1.
=1+(n-1)×2=2n-1.
从而由an=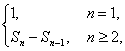 得an=
得an=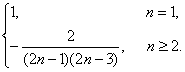

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
题目内容
已知数列{an}中,a1=1,且Sn=
思路分析:已知条件是一个关于Sn的递推式,可以先求出Sn,然后求an.
解:由Sn=∴{![]() }是首项为
}是首项为![]() =
=![]() =1,公差为2的等差数列.∴
=1,公差为2的等差数列.∴![]() =1+(n-1)×2=2n-1.
=1+(n-1)×2=2n-1.
从而由an=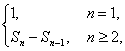 得an=
得an=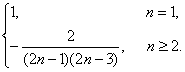

A、
| ||
B、
| ||
C、
| ||
D、
|