题目内容
若AB是过椭圆 中心的一条弦,M是椭圆上任意一点,且AM,BM与坐标轴不平行,kAM,kBM分别表示直线AM,BM的斜率,则kAM•kBM=
中心的一条弦,M是椭圆上任意一点,且AM,BM与坐标轴不平行,kAM,kBM分别表示直线AM,BM的斜率,则kAM•kBM=
- A.

- B.
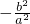
- C.

- D.

B
分析:假设点的坐标,将斜率用坐标表示,再将A,M的坐标代入椭圆方程可求
解答:设A(x1,y1),M(x0,y0),则B(-x1,-y1),则kAM•kBM=
∵A,M在椭圆上,
∴ ,
, ,两式相减,可得KAM•KBM=-
,两式相减,可得KAM•KBM=-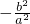 ,
,
故选B.
点评:本题主要考查了圆锥曲线的共同特征.考查了学生综合分析问题和解决问题的能力.
分析:假设点的坐标,将斜率用坐标表示,再将A,M的坐标代入椭圆方程可求
解答:设A(x1,y1),M(x0,y0),则B(-x1,-y1),则kAM•kBM=

∵A,M在椭圆上,
∴
 ,
, ,两式相减,可得KAM•KBM=-
,两式相减,可得KAM•KBM=-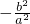 ,
,故选B.
点评:本题主要考查了圆锥曲线的共同特征.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
(2007
武汉模拟)若AB是过椭圆 中心的弦,
中心的弦, 为椭圆的焦点,则
为椭圆的焦点,则 面积的最大值为
面积的最大值为
[
]|
A .6 |
B .12 |
C .24 |
D .48 |
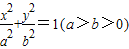 中心的一条弦,M是椭圆上任意一点,且AM,BM与坐标轴不平行,kAM,kBM分别表示直线AM,BM的斜率,则kAM•kBM=( )
中心的一条弦,M是椭圆上任意一点,且AM,BM与坐标轴不平行,kAM,kBM分别表示直线AM,BM的斜率,则kAM•kBM=( )
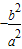
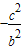
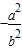
 中心的一条弦,M是椭圆上任意一点,且AM,BM与坐标轴不平行,kAM,kBM分别表示直线AM,BM的斜率,则kAM•kBM=( )
中心的一条弦,M是椭圆上任意一点,且AM,BM与坐标轴不平行,kAM,kBM分别表示直线AM,BM的斜率,则kAM•kBM=( )


