题目内容
已知f(x)是偶函数,且在(0,+∞)上是增函数,当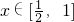 时,不等式f(ax+1)≤f(x-3)恒成立,则实数a的取值范围是
时,不等式f(ax+1)≤f(x-3)恒成立,则实数a的取值范围是
- A.[-3,3]
- B.[-7,1]
- C.[-7,3]
- D.[-3,1]
D
分析:由已知中f(x)是偶函数,,且f(x)在(0,+∞)上是增函数,由偶函数在对称区间上单调性相反,易得f(x)在(-∞,0)上为减函数,又由若x∈[ ,1]时,不等式f(ax+1)≤f(x-3)恒成立,结合函数恒成立的条件,可以构造一个关于a的不等式,解不等式即可得到实数a的取值范围.
,1]时,不等式f(ax+1)≤f(x-3)恒成立,结合函数恒成立的条件,可以构造一个关于a的不等式,解不等式即可得到实数a的取值范围.
解答:∵f(x)是偶函数,且f(x)在(0,+∞)上是增函数
∴f(x)在(-∞,0)上为减函数
当x∈[ ,1]时
,1]时
x-3∈[ ,-2]
,-2]
故f(x-3)≥f(2)
若x∈[ ,1]时,不等式f(ax+1)≤f(x-3)恒成立,
,1]时,不等式f(ax+1)≤f(x-3)恒成立,
则当x∈[ ,1]时,|ax+1|≤2恒成立
,1]时,|ax+1|≤2恒成立
解得-3≤a≤1
故选D
点评:本题考查的知识点是奇偶性与单调性的综合,其中根据已知条件结合偶函数在对称区间上单调性相反,证得f(x)在(-∞,0)上为减函数,进而给出x∈[ ,1]时f(x-3)的最小值,是解答本题的关键,属中档题.
,1]时f(x-3)的最小值,是解答本题的关键,属中档题.
分析:由已知中f(x)是偶函数,,且f(x)在(0,+∞)上是增函数,由偶函数在对称区间上单调性相反,易得f(x)在(-∞,0)上为减函数,又由若x∈[
 ,1]时,不等式f(ax+1)≤f(x-3)恒成立,结合函数恒成立的条件,可以构造一个关于a的不等式,解不等式即可得到实数a的取值范围.
,1]时,不等式f(ax+1)≤f(x-3)恒成立,结合函数恒成立的条件,可以构造一个关于a的不等式,解不等式即可得到实数a的取值范围.解答:∵f(x)是偶函数,且f(x)在(0,+∞)上是增函数
∴f(x)在(-∞,0)上为减函数
当x∈[
 ,1]时
,1]时x-3∈[
 ,-2]
,-2]故f(x-3)≥f(2)
若x∈[
 ,1]时,不等式f(ax+1)≤f(x-3)恒成立,
,1]时,不等式f(ax+1)≤f(x-3)恒成立,则当x∈[
 ,1]时,|ax+1|≤2恒成立
,1]时,|ax+1|≤2恒成立解得-3≤a≤1
故选D
点评:本题考查的知识点是奇偶性与单调性的综合,其中根据已知条件结合偶函数在对称区间上单调性相反,证得f(x)在(-∞,0)上为减函数,进而给出x∈[
 ,1]时f(x-3)的最小值,是解答本题的关键,属中档题.
,1]时f(x-3)的最小值,是解答本题的关键,属中档题. 
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知f(x)是偶函数,且f(x)在[0,+∞)上是增函数,如果f(ax+1)≤f(x-2)在x∈[
,1]上恒成立,则实数a的取值范围是( )
| 1 |
| 2 |
| A、[-2,1] |
| B、[-5,0] |
| C、[-5,1] |
| D、[-2,0] |