题目内容
已知函数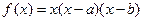 。
。
(1)若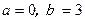 ,函数
,函数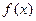 在
在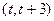 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求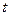 的取值范围;
的取值范围;
(2)当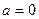 时,
时,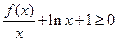 对任意的
对任意的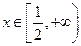 恒成立,求
恒成立,求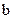 的取值范围;
的取值范围;
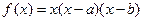 。
。(1)若
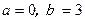 ,函数
,函数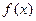 在
在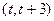 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求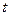 的取值范围;
的取值范围;(2)当
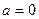 时,
时,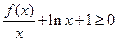 对任意的
对任意的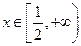 恒成立,求
恒成立,求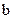 的取值范围;
的取值范围;解:(Ⅰ)当 时
时 ………………2分
………………2分
 在
在 上递增,在
上递增,在 上递减
上递减
所以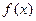 在0和2处分别达到极大和极小,由已知有
在0和2处分别达到极大和极小,由已知有
 且
且 ,因而
,因而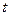 的取值范围是
的取值范围是 . …………………………4分
. …………………………4分
(Ⅱ)当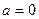 时,
时, 即
即
可化为
 ,记
,记
则 …………………………8分
…………………………8分
记 则
则 ,
,
 在
在 上递减,在
上递减,在 上递增.
上递增.

从而 上递增
上递增
因此 故
故
 时
时 ………………2分
………………2分 在
在 上递增,在
上递增,在 上递减
上递减所以
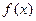 在0和2处分别达到极大和极小,由已知有
在0和2处分别达到极大和极小,由已知有 且
且 ,因而
,因而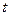 的取值范围是
的取值范围是 . …………………………4分
. …………………………4分(Ⅱ)当
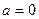 时,
时, 即
即
可化为

 ,记
,记
则
 …………………………8分
…………………………8分记
 则
则 ,
, 在
在 上递减,在
上递减,在 上递增.
上递增.
从而
 上递增
上递增因此
 故
故
略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
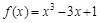 在闭区间[-3,0]上的最大值、最小值分别是 .
在闭区间[-3,0]上的最大值、最小值分别是 .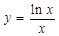 的最大值为( )
的最大值为( )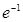



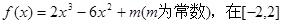 上有最大值为3,则f(x)在[-2,2]上的最小值为
上有最大值为3,则f(x)在[-2,2]上的最小值为 ,若函数
,若函数 的极值点小于零,则( )
的极值点小于零,则( )



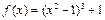 的极值是 ( )
的极值是 ( )
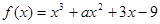 ,已知
,已知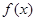 在
在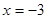 时取得极值,则
时取得极值,则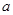 = ▲ .
= ▲ .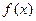 的最小值为3,且当
的最小值为3,且当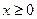 时,
时,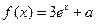 ,其中e是自然对数的底数
,其中e是自然对数的底数 。
。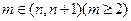 使得存在
使得存在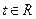 ,只要
,只要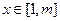 ,就有
,就有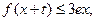 求正整
求正整