题目内容
设数列{an}是等差数列,a5=6
(1)当a3=3时,在数列{an}中找一项am,使a3,a5,am成等比数列,求m的值;
(2)当a3=2时,若自然数nt(t=1,2,3,…),满足5<n1<n2<…<nt<…,且使得 …成等比数列,求数列{nt}的表达式.
…成等比数列,求数列{nt}的表达式.
解:(1)由于a5=a3+2d 所以d= am=a3+(m-3)d=
am=a3+(m-3)d= (m-1)
(m-1)
∵a3、a5、am成等比数列∴36=3× (m-1)
(m-1)
∴m=9.
(2)由a3=2,a5=6,∴d=2∴an=a3+(n-3)d=2n-4
又 公比q= ∴
∴ =2×3t+1∴2nt-4=2×3t+1∴nt=3t+1+2.
=2×3t+1∴2nt-4=2×3t+1∴nt=3t+1+2.
分析:(1)设出等差数列的公差,利用a5=a3+2d,求出d,a3,a5,am成等比数列,求出m即可.
(2)利用a3=2,a5=6,求出d,然后求出公比,通过 …成等比数列,求出数列{nt}的表达式.
…成等比数列,求出数列{nt}的表达式.
点评:本题是中档题,考查等差数列与等比数列的关系,考查计算能力.
 am=a3+(m-3)d=
am=a3+(m-3)d= (m-1)
(m-1)∵a3、a5、am成等比数列∴36=3×
 (m-1)
(m-1)∴m=9.
(2)由a3=2,a5=6,∴d=2∴an=a3+(n-3)d=2n-4
又 公比q=
 ∴
∴ =2×3t+1∴2nt-4=2×3t+1∴nt=3t+1+2.
=2×3t+1∴2nt-4=2×3t+1∴nt=3t+1+2.分析:(1)设出等差数列的公差,利用a5=a3+2d,求出d,a3,a5,am成等比数列,求出m即可.
(2)利用a3=2,a5=6,求出d,然后求出公比,通过
 …成等比数列,求出数列{nt}的表达式.
…成等比数列,求出数列{nt}的表达式.点评:本题是中档题,考查等差数列与等比数列的关系,考查计算能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
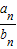 }的前n项和Sn.
}的前n项和Sn.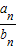 }的前n项和Sn.
}的前n项和Sn.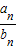 }的前n项和Sn.
}的前n项和Sn.