题目内容
2.若点M在△ABC的边AB上,且$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{MB}$,则$\overrightarrow{CM}$=( )| A. | $\frac{1}{2}$$\overrightarrow{CA}$+$\frac{1}{2}$$\overrightarrow{CB}$ | B. | 2$\overrightarrow{CA}$-2$\overrightarrow{CB}$ | C. | $\frac{1}{3}$$\overrightarrow{CA}$+$\frac{2}{3}$$\overrightarrow{CB}$ | D. | $\frac{2}{3}$$\overrightarrow{CA}$+$\frac{1}{3}$$\overrightarrow{CB}$ |
分析 如图,$\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}$=$\overrightarrow{CA}+\frac{1}{3}\overrightarrow{AB}$=$\overrightarrow{CA}+\frac{1}{3}(\overrightarrow{CB}-\overrightarrow{CA})$=$\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$.
解答 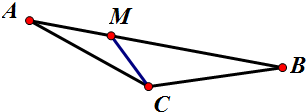 解:如图,由$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{MB}$,知$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,
解:如图,由$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{MB}$,知$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,
所以$\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}$
=$\overrightarrow{CA}+\frac{1}{3}\overrightarrow{AB}$
=$\overrightarrow{CA}+\frac{1}{3}(\overrightarrow{CB}-\overrightarrow{CA})$
=$\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$
故选:D.
点评 本题考查向量的加减法运算法则,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在等差数列{an}中,a7=8,前7项和S7=42,则其公差是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
10.已知抛物线 y2=2px(p>0)的焦点为F,准线为 l,过点F的直线交抛物线于A,B两点,过点A作准线l的垂线,垂足为E,当A点坐标为 (3,y0)时,△AEF为正三角形,则此时△OAB的面积为( )
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{5\sqrt{3}}}{3}$ |
7.下面是关于复数z=$\frac{2}{1-i}$的四个命题:p1:|z|=2,p2:z2=2i,p3:z的共轭复数为-1+i,p4:z的虚部为1,其中真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |