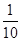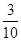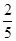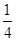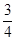题目内容
已知函数 ,其中
,其中 ,则使得
,则使得 在
在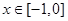 上有解的概率为( )
上有解的概率为( )
A. | B. | C.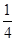 | D. |
A
解析试题分析:根据已知函数函数 ,其中
,其中 ,则使得
,则使得 ,分别对于a,b进行赋值可知,
,分别对于a,b进行赋值可知, ,故可知
,故可知 ,那么
,那么 ,那么可知
,那么可知 ,只要b=1,b=2在
,只要b=1,b=2在 时都成立,可知在
时都成立,可知在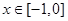 上有解的概率为
上有解的概率为 ,选A.
,选A.
考点:古典概型概率计算
点评:解决该试题的关键是能利用不等式得到x的解集,然后来分析解集与区间[-1,0]的长度的比值即可,属于基础题。

练习册系列答案
相关题目
从装有 个红球和
个红球和 个黒球的口袋内任取
个黒球的口袋内任取 个球,那么互斥而不对立的两个事件是
个球,那么互斥而不对立的两个事件是
| A.至少有一个黒球与都是红球 | B.至少有一个黒球与都是黒球 |
C.至少有一个黒球与至少有 个红球 个红球 | D.恰有 个黒球与恰有 个黒球与恰有 个黒球 个黒球 |
设随机变量X~ ,则P(X=3)的值是( )
,则P(X=3)的值是( )
A. | B. | C. | D. |
下列说法正确的是
| A.互斥事件一定是对立事件,对立事件不一定是互斥事件 |
| B.互斥事件不一定是对立事件,对立事件一定是互斥事件 |
C.事件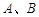 中至少有一个发生的概率一定比 中至少有一个发生的概率一定比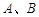 中恰有一个发生的概率大 中恰有一个发生的概率大 |
D.事件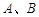 同时发生的概率一定比 同时发生的概率一定比 中恰有一个发生的概率小 中恰有一个发生的概率小 |
在棱长为 的正方体
的正方体 内任取一点
内任取一点 ,则点
,则点 到点
到点 的距离小等于
的距离小等于 的概率为
的概率为
A. | B. | C. | D. |
已知ξ~N(0,62),且P(-2≤ξ≤0)=0.4,则P(ξ>2)等于( )
| A.0.1 | B.0.2 | C.0.6 | D.0.8 |