Question

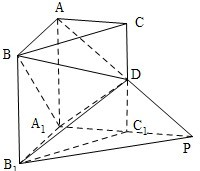如图，在直三棱柱ABC-A₁B₁C₁中，∠BAC=90°，AB=AC=AA₁=1，D是棱CC₁上的一点，P是AD的延长线与A₁C₁的延长线的交点，且PB₁∥平面BDA₁
（Ⅰ）求证：CD=C₁D；
（Ⅱ）求二面角A-A₁D-B的平面角的余弦值；
（Ⅲ）求点C到平面B₁DP的距离．

Answer 1

分析：（I）°由题意及图形建立空间直角坐标系，写出相应点的坐标，利用AC∥PC₁，建立点D的汗有未知数x的坐标，利用PB₁∥平面BDA₁建立x的方程，解出即证出所求；
（II）由题意及（I）所建立的坐标系，利用平面法向量与二面角的大小之间的关系求出二面角的大小；
（III）利用空间向量中求带到平面的距离公式直接求出点到平面的距离．

解答：解：（I）由题意作出如下图形并建立图示的空间直角坐标系：
以A₁点为原点，A₁B₁，A₁C₁，A₁A所在的直线分别为x，y，z轴，
建立图示的空间直角坐标系，则A₁（0，0，0）B₁（1，0，0）C₁（0，1，0）B（1，0，1）
（I）设C₁D=x，
∵AC∥PC₁
∴

C1P

AC

=

C1D

CD

=

x

1-x

可设D（0，1，x），则P(0，1+

x

1-x

，0)，
∴

A1B

=(1，0，1)   

A1D

=（0，1，x），

B1P

=(-1，1+

x

1-x

，0)   
设平面BA₁D的一个法向量为

n

=（a，b，c），
则

n • A1B =0 n • A1D =0

?

a+c=0 b+cx=0

  令a=1，则

n

=（1，x，-1）∵PB₁∥平面BA₁D
∴

n •

B1P

=1×(-1)+x•(1+

x

1-x

)+(-1)×0=0?x=

1

2

；
故CD=C₁D．

（II）由（I）知，平面BA₁D的一个法向量为

n

=(1，

1

2

，-1) 
又

m

=（1，0，0）为平面AA₁D的一个法向量，∴cos＜

n

，

m

＞=

n • m

| n |•| m|

=

2

3

．
故二面角A-A₁D-B的平面角的余弦值为

2

3

．
（III）∵

PB1

=(1，-2，0)，

PD

=(0，-1，

1

2

)  
设平面B₁DP的一个法向量为

p

=（x，y，z），
则

p • PB1 =0 p • PD =0

?

x-2y=0 -y+ z 2 =0

 
令z=1，∴

p

=(1，

1

2

，1) 
又

DC

=(0，0，

1

2

)∴C到平面B₁PD的距离d=

| DC • p |

|p |

=

1

3

．

点评：此题重点考查了利用空间向量的方法求点到平面的距离和二面角的大小，还考查了利用方程的思想求解坐标中所设的变量的大小．