题目内容
如图,在矩形ABCD中,AB=2,AD=1,E是CD的中点,以AE为折痕将△DAE向上折起,使D为D′,且平面D′AE⊥平面ABCE

(Ⅰ)求证:AD′⊥EB;
(Ⅱ)求二面角D′-AC-B的大小;
(Ⅲ)求点C到面D′BE的距离.

(Ⅰ)求证:AD′⊥EB;
(Ⅱ)求二面角D′-AC-B的大小;
(Ⅲ)求点C到面D′BE的距离.
分析:(Ⅰ)要证AD′⊥EB,只需证明EB⊥平面AD′E,只需证明AE⊥EB,MD′⊥BE即可;
(Ⅱ)过M作MN⊥AC于N,连接D′N,则∠MND′为二面角D′-AC-B的大小,通过解三角形即可求二面角D′-AC-B的大小;
(Ⅲ)利用VD′-BCE=VC-BED′,体积相等直接求点C到面D′BE的距离.
(Ⅱ)过M作MN⊥AC于N,连接D′N,则∠MND′为二面角D′-AC-B的大小,通过解三角形即可求二面角D′-AC-B的大小;
(Ⅲ)利用VD′-BCE=VC-BED′,体积相等直接求点C到面D′BE的距离.
解答:解:如图所示: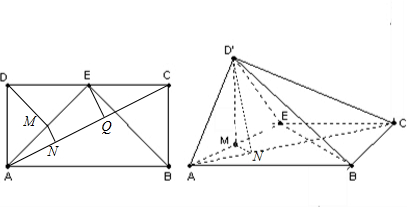
(Ⅰ)证明:因为AE=EB=
,AB=2,所以AB2=AE2+BE2,即AE⊥EB,
取AE的中点M,连接MD′,则AD=D′E⇒MD′⊥AE,
又平面D′AE⊥平面ABCE,可得MD′⊥平面ABCE,即得MD′⊥BE,
从而EB⊥平面AD′E,故AD′⊥EB …(4分)
(Ⅱ)过M作MN⊥AC于N,连接D′N,则∠MND′为二面角D′-AC-B的大小,
MN=
EQ=
×
=
;DM=
,
二面角D′-AC-B的大小为tan∠MND′=
=
,
所以∠MND′=arctan
; …(8分)
(Ⅲ)因为VD′-BCE=VC-BED′,
即
×SBED′×h=
×SBCE×DM,
h=
=
,
点C到面BED′的距离是0.5.…(12分)

(Ⅰ)证明:因为AE=EB=
| 2 |
取AE的中点M,连接MD′,则AD=D′E⇒MD′⊥AE,
又平面D′AE⊥平面ABCE,可得MD′⊥平面ABCE,即得MD′⊥BE,
从而EB⊥平面AD′E,故AD′⊥EB …(4分)
(Ⅱ)过M作MN⊥AC于N,连接D′N,则∠MND′为二面角D′-AC-B的大小,
MN=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 | ||
|
| ||
| 10 |
| ||
| 2 |
二面角D′-AC-B的大小为tan∠MND′=
| ||||
|
| 10 |
所以∠MND′=arctan
| 10 |
(Ⅲ)因为VD′-BCE=VC-BED′,
即
| 1 |
| 3 |
| 1 |
| 3 |
h=
| ||||||
|
| 1 |
| 2 |
点C到面BED′的距离是0.5.…(12分)
点评:本题是中档题,考查直线与直线的垂直的证明,二面角的求法,点到平面的距离的求法,考查空间想象能力,转化思想,计算能力.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD. 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点. 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=