题目内容
已知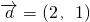 ,
, ∥
∥ ,
, •
• =10,则
=10,则 =________.
=________.
2
分析:利用两个向量共线的性质可得 =(2λ,λ ),再由向量的模的定义可得
=(2λ,λ ),再由向量的模的定义可得  =
= ,运算求得结果.
,运算求得结果.
解答:由题意可得 =λ
=λ  ,则由
,则由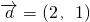 可得
可得  =(2λ,λ ).
=(2λ,λ ).
∴ =(2,1)•(2λ,λ )=4λ+λ=5λ=10,∴λ=2.
=(2,1)•(2λ,λ )=4λ+λ=5λ=10,∴λ=2.
∴ =(4,2),
=(4,2),
∴ =
= =2
=2 .
.
故答案为:2 .
.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,向量的模的定义,属于基础题.

分析:利用两个向量共线的性质可得
 =(2λ,λ ),再由向量的模的定义可得
=(2λ,λ ),再由向量的模的定义可得  =
= ,运算求得结果.
,运算求得结果.解答:由题意可得
 =λ
=λ  ,则由
,则由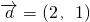 可得
可得  =(2λ,λ ).
=(2λ,λ ).∴
 =(2,1)•(2λ,λ )=4λ+λ=5λ=10,∴λ=2.
=(2,1)•(2λ,λ )=4λ+λ=5λ=10,∴λ=2.∴
 =(4,2),
=(4,2),∴
 =
= =2
=2 .
.故答案为:2
 .
.点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,向量的模的定义,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目